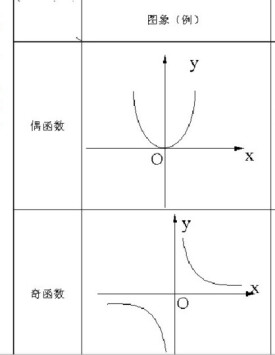
奇函數

在奇函數中，和的符號相反且絕對值相等，即，＝，

反之，滿足＝的函數一定是奇函數。例如:

1. 兩個奇函數相加所得的和或相減所得的差為奇函數。

2. 一個偶函數與一個奇函數相加所得的和或相減所得的差為非奇非偶函數。

3. 兩個奇函數相乘所得的積或相除所得的商為偶函數。

4. 一個偶函數與一個奇函數相乘所得的積或相除所得的商為奇函數。

5. 當且僅當（定義域關於原點對稱）時，既是奇函數又是偶函數。奇函數在對稱區間上的積分為零。

1、奇函數圖象關於原點對稱。

2、奇函數的定義域必須關於原點對稱，否則不能成為奇函數。

3、若為奇函數，且在x=0處有意義，則.

4、設在定義域上可導，若在上為奇函數，則在上為偶函數。

即＝對其求導

若用-x代替x,函數保持不變，則稱這樣的函數為偶函數(拉丁文functionespares)。歐拉列舉了三類偶函數和三類奇函數，並討論了奇偶函數的性質。法國數學家達朗貝爾(J.R.D.Alembert，1717-1783)在狄德羅(D.Diderot,1713-1784)主編的《大百科全書》第7卷（1757年出版）關於函數的詞條中說：“古代幾何學家，更確切地說是古代分析學家，將某個量x的不同次冪稱為x的函數．”類似地，法國數學家拉格朗日《解析函數論》（1797）開篇中也說，早期分析學家們使用“函數”這個詞，只是表示“同一個量的不同次冪”，後來，其涵義被推廣，表示“以任一方式得自其他量的所有量”，萊布尼茨和約翰·伯努利最早採用了后一涵義。在1727年的論文中，歐拉在討論奇、偶函數時確實沒有涉及任何超越函數。因此，最早的奇、偶函數概念都是針對冪函數以及相關複合函數而言，歐拉提出的“奇函數”、“偶函數”之名顯然源於冪函數的指數或指數分子的奇偶性：指數為偶數的冪函數為偶函數，指數為奇數的冪函數為奇函數。

1748年，歐拉出版他的數學名著《無窮分析引論》，將函數確立為分析學的最基本的研究對象．在第一章，他給出了函數的定義、對函數進行了分類，並再次討論了兩類特殊的函 數：偶函數和奇函數。歐拉給出的奇、偶函數定義與1727年論文中的定義實質上並無二致，但他討論了更多類型的奇、偶函數，也給出了奇函數的更多的性質。

歐拉認為，函數與函數是等價的，所以儘管奇函數與偶函數的乘積為奇函數，但有時這樣的乘積也可能會是偶函數。鑒於此，歐拉提出，要使一個偶函數的冪仍為偶函數，就必須對冪指數進行限制，特別的，如果指數為分數，那麼它的分母就不能為偶數。在將偶函數定義為的複合函數時，歐拉特別增加了一個限制條件：中不能含有之類的根式。顯然，歐拉未能區別函數和函數。

雖然達朗貝爾在《大百科全書》中給出了函數的定義，並介紹了有理函數、無理函數、齊次函數、相似函數，但隻字未提“奇函數”和“偶函數”這兩種特殊函數。

1786年，法國人裴奇（F.pezzi）將《無窮分析引論》第1卷譯成了法文，“奇函數”和“偶函數”分別被譯為“fonction paire”“fonction impaire”,這是兩個數學名詞在法文中的首次出現。

1792年，法國數學家勒讓德（A.Legendre）(1752-1833)向科學院提交論文“關於橢圓超越性”中提出了“正弦函數的偶函數”。勒讓德可能沿用了裴奇的譯名或直接翻譯了歐拉的名詞。這裡我們需要指出的是，將“偶函數”“奇函數”的拉丁文翻譯成對應的法文，並不會產生不同的譯法，因為最遲在笛卡兒（R.Descartes,1596-1650）的《幾何學》中已經有了法文的“偶數”（nombres pairs）和“奇數”(nombres impairs)之名。

“奇函數”、“偶函數”這兩個名稱在18世紀末的法國並未得到普遍使用；或者說，函數的奇偶性還沒有受到當時法國數學家的普遍關注。1796年，法國數學家拉貝將《無窮分析引論》全書譯成法文，其中拉貝同樣將“奇函數”、“偶函數”分別譯為“fonction paire”“fonction impaire”

1809年，蘇格蘭數學家華里司（W.Wallace,1768-1843）將勒讓德的論文譯成英文，發表在《數學文庫》(MathematicsRepository)上。華里司很自然地將“function paire”譯為“even function”。這是“even function”這個詞在英語世界中的首次出現。不過，在英國著名數學家胡頓（C.Hutton，1737-1823）於1815年出版的《數學與哲學辭典》中，雖然有“函數”和“微積分中的函數”這兩個詞條，但奇、偶函數念卻付之闕如。而德摩根的《代數學基礎》（偉烈亞力和李善蘭譯為《代數學》）雖對函數進行了清晰地分類，但仍隻字未提奇、偶函數。在美國，數學家羅密士（E.Loomis,1811-1889）的微積分暢銷書《解析幾何與微積分基礎》（李善蘭與偉烈亞力譯為《代微積拾級》）雖然給出了隱函數、顯函數、增函數、減函數之名，但同樣不含奇、偶函數之說。這說明，奇、偶函數概念以及華里司所引入的新名詞在19世紀上半葉的英語世界里尚未得到廣泛傳播和普遍關注．相應地，兩個概念也就不見於中國晚清的西方數學譯著。直到20世紀初，兩個概念才傳入中國。1938年出版的《算學名辭彙編》和1945年出版的《數學名詞》中都收錄了兩個名詞。

奇函數：，當在處有定義時，必有。

常見的奇函數有等。

對於函數，當時，既是奇函數又是偶函數，當時，是奇函數；當時，是偶函數。