斯圖爾特定理
斯圖爾特定理
在幾何學中，斯圖爾特定理(Stewart's theorem)給出了邊長和三角形中的cevian長度之間的關係，它的名字是為了紀念蘇格蘭數學家馬修斯圖爾特（Matthew Stewart），他在1746年發表了這個定理，與阿波羅尼奧斯定理相關。
在幾何學中，斯圖爾特定理表示了一個三角形中切氏線（cevian），連結一個頂點和對邊上任意一點的線段的長度和三角形三邊長的關係。它由蘇格蘭數學家MatthewStewart在1746年發表，故得名。
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
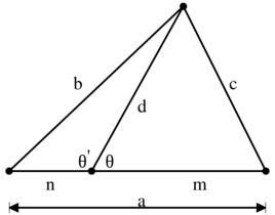
設、和是三角形邊長，表示邊長的cevian長度，如果cevian劃分邊長的長度為和，與毗鄰，與毗鄰，然後斯圖爾特定理說明如下：
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
可以使用帶符號的線段長度更加對稱地寫出該定理。即，取長AB為正或負，根據到是向左或右來選取。在這個公式中，該定理指出，如果，和是共線點，是任意點，那麼
斯圖爾特定理
該定理可以證明是餘弦定律的應用。
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
設是和之間的角度，是和之間的角度，然後是的補角，因此，根據角度在兩個小三角形餘弦定理和產生公式如下：
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
第一方程乘以，第二方程乘以，再相加添消除COSθ，可得到：
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
斯圖爾特定理
或者可以通過繪製從三角形頂點到基底的垂線來證明該定理，並使用畢達哥拉斯定理以高度來寫出距離、和，然後等式左側和右側的代數地減少到相同的表達式。
本定理可以用於各種三角形內切氏線的求長，而無論其位置。取定理的特殊情況，即可輕易求出三角形的中線長、高線長、角平分線長。
基本信息
- 中文名
- 斯圖爾特定理
- 外文名
- Stewart's theorem
- 應用學科
- 數學適用
- 提出時間
- 1746年
- 提出者
- Matthew Stewart
- 表達式
- mb^2+nc^2=a(d^2+mn).
- 領域範圍
- 平面幾何