前序遍歷
計算機科學術語之一
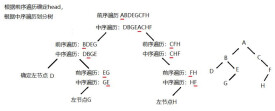
前序遍歷首先訪問根結點然後遍歷左子樹,最後遍歷右子樹。在遍歷左、右子樹時,仍然先訪問根結點,然後遍歷左子樹,最後遍歷右子樹。
若二叉樹為空則結束返回,否則:
(1)訪問根結點。
(2)前序遍歷左子樹。
前序遍歷
需要注意的是:遍歷左右子樹時仍然採用前序遍歷方法。
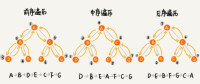
如右圖所示二叉樹
前序遍歷結果:ABDECF
已知後序遍歷和中序遍歷,就能確定前序遍歷。
當對一棵數學表達式樹進行中序,前序和後序遍歷時,就分別得到表達式的中綴、前綴和後綴形式。
因此,在前綴和後綴表達式中都不必採用括弧或優先順序。從左到右或從右到左掃描表達式並採用操作數棧,可以很容易確定操作數和操作符的關係。若在掃描中遇到一個操作數,把它壓入堆棧,若遇到一個操作符,則將其與棧頂的操作數相匹配。把這些操作數推出棧,由操作符執行相應的計算,並將所得結果作為操作數壓入堆棧。
設二叉樹中元素數目為n。這四種遍歷演演算法的空間複雜性均為O(n),時間複雜性為O(n)。
當t的高度為n時(右斜二叉樹的情況),通過觀察其前序、中序和後序遍歷時所使用的遞歸棧空間即可得到上述結論。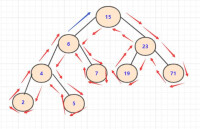

前序遍歷
樹節點結構和演演算法:
調用時:
核心代碼:
procedure first(i:longint);
begin
write(a[i]);
if a[i*2]<>0 then first(i*2);
if a[i*2+1]<>0 then first(i*2+1);
end;
二叉樹定義
遞歸實現
非遞歸實現