電磁振蕩

周期等於2π倍的根號下自感係數與電容的乘積。

如果電路中除電容、電感外還有電阻，即有能量損耗，但無電源，則電流和電荷的振幅逐漸衰減為零，開始時儲存的電磁場能通過電阻上散發的焦耳熱不斷損耗殆盡。這種電磁振蕩稱為阻尼振蕩。如果在由電容、電感和電阻組成的電路中還有交流電源，電源的電動勢隨時間按正弦或餘弦函數變化，則由於電源不斷提供能量，補償在電阻上的能量損耗，穩定后電路中電流、電荷的振幅將保持恆定。這種電磁振蕩稱為受迫振蕩，受迫振蕩的頻率等於交流電源的頻率。電磁振蕩的上述特徵在一些電磁測量儀錶（如靈敏電流計，衝擊電流計）中有重要應用。

電容器通過自感線圈放電，由於自感作用總是阻礙電流的變化，所以電路里的電流不能立刻達到最大值，而是由零逐漸增大．這時，線圈周圍的磁場逐漸增強，電容器里的電場因極板上電荷逐漸減少而逐漸減弱。這樣，電路里的電場能逐漸轉化為磁場能．當電容器放電完畢，Q=0時，電路中的電流達到最大值，電場能全部轉化為磁場能．

電容器放電完畢，由於自感作用，電路中仍然保持有原來方向的電流，但逐漸減弱，這樣就使電容器逐漸充電，不過兩極所帶的電荷符號都跟原來的相反．充電完畢，電流減小到零，磁場能全部轉化為電場能．

此後，上述的全部過程反覆地循環下去，在電路中就出現了振蕩電流．這種電場和磁場的周期性變化叫做電磁振蕩．在電磁振蕩的過程中，電場能和磁場能同時發生周期性的轉化．

電磁系統中，儲能元件內電能與磁能不斷相互轉換的過程叫做電磁振蕩；若系統受到外界周期性的電磁激勵，且激勵的頻率等於系統的自由振蕩頻率，則系統與激勵源間形成電諧振。

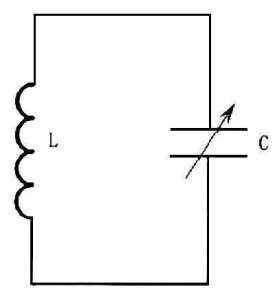
產生電磁振蕩的最簡單的實例是由電阻 R、電感線圈 L和電容器 C所組成的振蕩迴路，使其電容器 C中儲存的電能與電感線圈 L中儲存的磁能不斷地相互轉換。單迴路振蕩電路如圖1所示，圖1a是串聯迴路，圖1b是並聯迴路。

1、周期：電磁振蕩完成一次周期性變化所需要的時間叫做周期。一秒鐘內完成的周期性變化的次數叫頻率。

2、在LC振蕩電路中，從研究得到：T=2π√CL f=π√CL

可見在LC迴路中，電路的頻率f和周期T是由線圈的自感係數L和電容器的電容C來決定的。在收音機的調頻中，若將可變電容器的動片旋入，則會使電容器的電容C增大，故收音機接收的頻率變小。

若電源電壓為 e( t)，迴路中電流為 i( t)，電容器上的電壓為 V( t)，則可建立如下迴路方程或自由振蕩 迴路方程中激勵電壓 e（ t）為零時，振蕩的性質決定於各參數 R、 L、 C之間的相對數值。①當 時，迴路電流和元件上電壓都將依時間 t按指數規律下降，即因迴路電阻太大，迴路儲存的能量不足以維持振蕩一周的消耗，從而不能形成振蕩。②當時，得到一般的自由衰減振蕩，式中稱為衰減常數，為有損耗時自由振蕩角頻率，為無損耗時的自由振蕩角頻率或固有頻率。

一般常用無量綱量作為度量迴路品質的參數，叫做品質因數。與 Q是表徵迴路特性的重要參數。 Q值可表示有損耗時自由振蕩角頻率對固有頻率的偏離程度。一般情況下， RLC迴路中 Q值均較大，約為10～10，即使取 Q的低值， ω與 也只差 ω的0.125%。所以，通常認為單振蕩迴路的自由振蕩頻率近似為式中 L的單位為亨， C的單位為法， f的單位為赫。衰減振蕩的衰減因子可表示為，可見經過一個振蕩周期，幅度將衰減e倍。參數有時稱為對數衰減，而稱為迴路的時間常數，通常以 τ表示。強迫振蕩 當 e( t)≠0時，設外源是按正弦變化的電壓源。用相量表示法，迴路電流可寫為式中 ω=2 πf， f是電源的激勵頻率，。迴路的阻抗 Z可表示為；是在 ω=時迴路的 Q值；是迴路的相對失諧。 δ=0時迴路與諧振源間發生諧振，且諧振在迴路的固有頻率上，這時電感線圈 L和電容器 C上的電壓都等於電源電壓的 Q倍。在很多實際應用中，常利用高 Q迴路獲得高壓。 δ≠0時，迴路失諧，被迫在電源頻率 f下振蕩。這時電流為,即失諧時，電流隨迴路的 Q值和相對失諧 δ的增大而下降。在諧振頻率（即迴路的固有頻率）附近（即 δ1時），有近似關係。以 Q0 δ為橫坐標，以的幅值、實部和虛部為縱坐標，可繪得如圖2所示的通用曲線。其峰值在δ=0點，相對幅值等於1。當 Q0 δ=±1/2 即 ω= (1±1/2 )時，相對幅值下降到，功率下降到1/2。這兩點稱為半功率點。兩半功率點之間所覆蓋的頻率範圍稱迴路的通頻帶。 值越大，則通頻帶越窄，迴路的選擇性越好；反之， 值越小，則通頻帶就越寬，迴路的選擇性越差。

由於電容器的損耗一般很小，圖1b中未表出。應用相量法，迴路兩端的阻抗為。詩 Z的電抗部分為零的頻率稱為諧振頻率，可得並聯諧振頻率 ωb等於,可見並聯諧振頻率 fb略小於串聯共振頻率f0，實際應用中，多認為 fb近似等於 f0。諧振時，迴路兩端阻抗為 Zb,稱並聯諧振電阻，它比迴路電阻 R大 Q娿倍。若電源是一恆流源，流入迴路的電流為；電感支路的電流為；電容支路的電流為，因與近似反相，且，從而迴路中大部分電流呈迴流形式，能量在電容與電感之間相互轉換，形成電磁振蕩。從電源輸入迴路的功率 Q娿 RI僅用來補償振蕩過程中的損耗。

從上述內容可知，當損耗很小時，串聯迴路與並聯迴路呈對偶關係。串聯諧振時電阻為最小，等於 R，迴路的電流為最大；並聯諧振時電阻近於最大，等於 L/ CR，迴路兩端電壓為最大。偏離了諧振點，各量均按通用曲線變化，僅縱坐標所指的變數不同而已。

兩個或多個具有相同或不同諧振頻率的單振蕩迴路通過耦合元件相互接連起來，可以構成複雜的振蕩系統，這種系統有時又稱耦合迴路。常用的一些雙耦合迴路如圖3所示。圖3a是利用互感M將兩個單振蕩迴路 LC和 LC耦合起來的迴路。用耦合係數表示兩個單振迴路耦合的鬆緊程度，0< K<1。 K值大表示緊耦合， K值小表示松耦合。圖4表示兩個具有相同的固有頻率和品質因數的迴路，耦合后在不同的 K值下 I2/ I2m隨 δ變化的通用曲線， δ的意義與不同。當 K=1時，諧振出現一個最大值的峰點當 K<1時，只有一個小於最大值的峰點； K>1時，則出現雙峰。振蕩時電能與磁能不僅在一個單迴路中相互轉換，而且還在迴路之間相互轉移，出現了比較複雜的振蕩現象。耦合迴路應用廣泛，常用於級間的耦合及濾波電路中。

1、大小和方向都做周期性迅速變化的電流叫做振蕩電流，產生振蕩電流的電路叫做振蕩電路。最簡單的振蕩電路是由電感線圈和電容器組成的，簡稱LC迴路。LC迴路中產生振蕩電流是由於電容器不斷充電和放電，該振蕩電流是按正弦規律變化的。

2、LC電路中電磁振蕩的產生過程

①放電過程：在放電過程中，q↓、u↓、E↓→i↑、B↑、E↑，電容器的電場能逐漸轉變成線圈的磁場能。由於線圈的自感作用，電流i是按正弦規律逐漸增大的，電流不會立刻達到最大值。放電結束時，q=0，E=0，i最大，E最大，電場能完全轉化成磁場能。

②充電過程：放電結束時，由於L的自感作用，電路中移動的電荷不會立即停止運動，仍保持原方向流動。在充電過程中，q↑、u↑、E↑→I↓、B↓、E↓，線圈的磁場能向電容器的電場能轉化。充電結束時，q、E增為最大，i、E均減小到零，磁場能向電場能轉化結束。

③反向放電過程：q↓、u↓、E↓→i↑、B↑、E↑，電容器的電場能轉化為線圈的磁場能。放電結束時，q=0，E=0，i最大，E最大，電場能向磁場能轉化結束。

④反向充電過程：q↑、u↑、E↑→i↓、B↓、E↓，與充電過程原理相同

LC電路，也稱為 諧振電路、槽路或 調諧電路，是包含一個電感（用字母L表示）和一個電容（用字母C表示）連接在一起的電路。該電路可以用作電諧振器（音叉的一種電學模擬），儲存電路共振時振蕩的能量。

LC電路既用於產生特定頻率的信號，也用於從更複雜的信號中分離出特定頻率的信號。它們是許多電子設備中的關鍵部件，特別是無線電設備，用於振蕩器、濾波器、調諧器和混頻器電路中。

電感電路是一個理想化的模型，因為它假定有沒有因電阻耗散的能量。任何一個LC電路的實際實現中都會包含組件和連接導線的儘管小卻非零的電阻導致的損耗。LC電路的目的通常是以最小的阻尼振蕩，因此電阻做得儘可能小。雖然實際中沒有無損耗的電路，但研究這種電路的理想形式對獲得理解和物理性直覺都是有益的。

在 LC電路中，L代表電感，單位：亨利（H），C代表電容，單位：法拉（F）。

電磁振蕩完成一次周期性變化需要的時間叫做周期，一秒內完成的周期性變化的次數叫做頻率。

振蕩電路中發生電磁振蕩時，如果沒有能量損失，也不受其他外界的影響，這是電磁振蕩的周期和頻率，叫做振蕩電路的固有頻率和固有周期。固有周期可以用下式求得

其時間常數為L/R.