梅涅勞斯定理
幾何學定理之一
梅涅勞斯（Menelaus）定理（簡稱梅氏定理）最早出現在由古希臘數學家梅涅勞斯的著作《球面學》（Sphaerica）中。
任何一條直線截三角形的各邊或其延長線，都使得三條不相鄰線段之積等於另外三條線段之積，這一定理同樣可以輕而易舉地用初等幾何或通過應用簡單的三角關係來證明. 梅涅勞斯把這一定理擴展到了球面三角形。
當一條直線交三邊所在的直線分別於點時，則有
過點A作AG∥DF交BC的延長線於點G.則
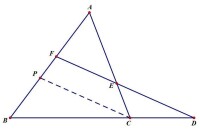
梅涅勞斯定理
過點C作CP∥DF交AB於P，則
兩式相乘得
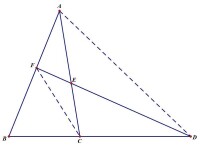
梅涅勞斯定理
得
× × = × ×
過三頂點作直線DEF的垂線AA‘，BB'，CC'，如圖：
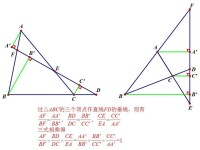
梅涅勞斯定理
充分性證明：
△ABC中，BC，CA，AB上的分點分別為D，E，F。
連接DF交CA於E'，則由充分性可得，
又∵
∴有，兩點重合。所以 共線
推論 在△ABC的三邊BC、CA、AB或其延長線上分別取L、M、N三點，又分比是λ= 、μ= 、ν= 。於是L、M、N三點共線的充要條件是。（注意與塞瓦定理相區分，那裡是）
此外，用該定理可使其容易理解和記憶：
第一角元形式的梅涅勞斯定理如圖：若E，F，D三點共線，則
即圖中的藍角正弦值之積等於紅角正弦值之積。
該形式的梅涅勞斯定理也很實用。
證明：可用面積法推出：第一角元形式的梅氏定理與頂分頂形式的梅氏定理等價。
第二角元形式的梅涅勞斯定理
在平面上任取一點O，且EDF共線，則 (O不與點A、B、C重合)
梅涅勞斯定理
作CH平行於AB交FD於點H
使用梅涅勞斯定理可以進行直線形中線段長度比例的計算，其逆定理還可以用來解決三點共線、三線共點等問題的判定方法，是平面幾何學以及射影幾何學中的一項基本定理，具有重要的作用。梅涅勞斯定理的對偶定理是塞瓦定理。
它的逆定理也成立：若有三點F、D、E分別在的邊AB、BC、CA或其延長線上，且滿足，則F、D、E三點共線。利用這個逆定理，可以判斷三點共線。
頂點到交點，交點回頂點。
若梅氏線完全在三角形外，那麼該三角形仍然成立。
基本信息
- 中文名
- 梅涅勞斯定理
- 外文名
- Menelaus
- 提出時間
- 古希臘時期，約公元236年
- 別名
- 梅氏定理、梅內勞斯定理
- 表達式
- (AF/FB)×(BD/DC)×(CE/EA)=1
- 提出者
- 應用學科
- 數學、物理
- 適用領域
- 平面幾何學，射影幾何學