效率矩陣
效率矩陣
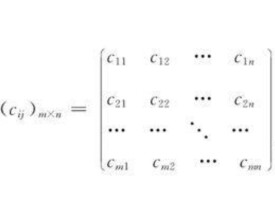
效率矩陣(efficiency matrix)亦稱價值矩陣,指派問題中的重要參數,是由指派問題的數學模型中元素cij(i=1,2,…,m;j=1,2,…,n)構成的矩陣。
效率矩陣

效率矩陣
效率矩陣
效率矩陣
定理1 設指派問題的效率矩陣為。若將該矩陣的某一行(或某一列)的各個元素都減去同一常數t(t可正可負),得到新的效率矩陣,則以C'為效率矩陣的新指派問題與原指派問題的最優解相同,但其最優值比原最優值減少t。
證明 設原指派問題的數學模型為
效率矩陣
效率矩陣
效率矩陣
效率矩陣
式(1)表示完成全部n項工作所消耗的總資源數最少;式(2)表示第i個人只能完成且必須完成一項工作;式(3)表示第j項工作只派一個人去且必須派一個人去完成;式(4)要求決策變數只取0或1兩個整數值。
現在矩陣C的第k行各元素都減去同一常數t,記新指派問題的目標函數為Z',則有
效率矩陣
效率矩陣
上式最後兩步,利用了式(2),因此有
效率矩陣
推論1 若將指派問題的效率矩陣每一行和每一列分別減去各行和各列的最小元素,則得到的新指派問題與原指派問題有相同的最優解。
證明 結論是顯然的,只要反覆運用定理1便可得證。
效率矩陣
效率矩陣
當將效率矩陣的每一行都減去各行的最小元素,將所得的矩陣的每一列再減去當前列中最小元素,則最後得到的新效率矩陣C'中必然會出現一些零元素。設,從第i行來看,它表示第i個人去干第j項工作效率(相對)最好。而從第j列來看,它表示第j項工作以第i個人來干效率(相對)最高。
定義 在效率矩陣C中,處在不同行不同列的一組零元素,稱為獨立零元素組,此時其中每個零元素稱為獨立零元素。
定理2 效率矩陣C中獨立零元素的最多個數等於能覆蓋所有零元素的最小直線數。