湍流的平均運動方程(見粘性不可壓縮流體動力學)。提出這一方程的
英國物理學家O.雷諾認為,粘性不可壓縮流體作湍流運動時,
流場中的瞬時參量:壓力p和速度分量u、v、w 仍舊滿足納維-斯托克斯方程,並可將該瞬時
參量分解為時間平均值p、u、v、w和在時間平均值上下漲落的脈動值p′、u′、v′、w′,將其代入上述方程並取時間平均后,可得到用平均量表示的湍流運動方程式。雷諾本人採用的是時間平均法,後人也有採用統計平均法的,這些都稱為雷諾方程。在
直角坐標系中,單位質量的平面流動雷諾方程是:在x方向投影:
雷諾方程
在y方向投影:
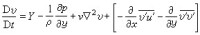
雷諾方程
方程的基本形式和各項物理意義都與
納維-
斯托克斯方程相同。由方括弧給出的最後一項是雷諾方程的特點,它反映由湍流動量轉化的應力(稱為
湍流應力),是未知量。因此,流動方程組不再封閉。1925年,德國物理學家L.普朗特提出
混合長度理論,後來人們又建立了各種
數學模型,力圖用流場的速度平均值來描述湍流應力,但仍未獲得統一的完善的模型,它仍然是
湍流理論研究的重要課題。