疲勞曲線
1860年維勒首先提出的概念
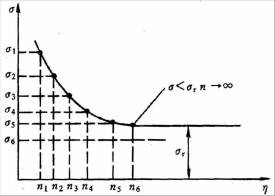
疲勞曲線是指金屬承受交變應力和斷裂循環周次之間的關係曲線。各種材料對變應力的抵抗能力,是以在一定循環作用次數N下,不產生破壞的最大應力σ-N來表示的。
σ-N稱為一定循環作用次數N的極限應力,也稱為條件疲勞極限。對於一種材料,根據實驗,可得出在各種循環作用次數N下的極限應力,以橫坐標為作用次數N、縱坐標為極限應力,繪成曲線,則稱為材料的疲勞曲線,或稱S-N曲線。
當應力低於某一值時,試樣可以經受無限次的循環而不斷裂。此應力值稱為該材料的疲勞極限,通常用σr來表示。註腳r表示應力循環對稱係數。假如是對稱循環的變應力,即r=-1;如是脈動循環時,即r=0。疲勞極限分為持久疲勞極限、有限疲勞極限。
對於一般具有應變時效的金屬材料,如碳鋼、合金結構鋼、球鐵等,當循環應力水平降低到某一臨界值時,低應力段變成水平線段,表示式樣可以經無限次應力循環也不發生疲勞斷裂,故將對應的應力稱為疲勞極限,記為σ-1。
所謂全疲勞曲線就是以疲勞極限圖的形式作出的一系列不同壽命的疲勞曲線,即由疲勞壽命、幅值應力、平均應力三個參數構成的疲勞壽命曲線,如圖4所示。
這種曲線可用於進行各種交變載荷或隨機載荷作用下零件疲勞壽命估算以及結構的內應力和預應力的估算,所以又把它叫做萬能疲勞曲線。
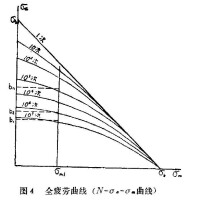
圖4
要作出這樣一系列曲線,當然要作大量的試驗工作。為了提高工作效率和節省試驗時間,根據試驗設備的具體情況,在一台設備上同時進行多個試件的疲勞試驗,不同的試件其應力幅值相同,平均應力不同,這樣一次就可得到同一應力幅下不同應力均值的一系列試驗數據,通過對一系列數據進行回歸分析,就可以得到同一應力幅下平均應力值與壽命關係的方程式。用相同的試驗方法和數據處理方法,就可以得到一系列不同應力幅值下,平均應力與壽命關係的回歸方程式,藉助於此方程式,就可以作出全疲勞曲線圖。考慮到試驗數據的分散性,應取可信度R=0.5的試驗數據來繪製該圖。在進行壽命估算時,直接查圖可能會帶來一些誤差,最理想的方法是將這些實測數據送入電子計算機,由計算機提供有關數據信息。
材料的疲勞特性曲線有兩種:σ-Ν曲線和等壽命曲線。