弧度制
用弧度作單位來度量角的制度
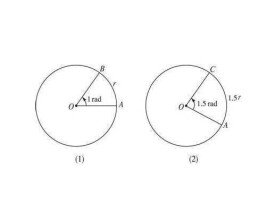
等於半徑長的圓弧所對的圓心角叫做1弧度的角,用符號rad表示,讀作弧度。用弧度作單位來度量角的制度叫做弧度制。另外一種度量角的方法是角度制。弧度制的精髓就在於統一了度量弧與半徑的單位,從而大大簡化了有關公式及運算,尤其在高等數學中,其優點就格外明顯。
在研究弧度制發展時,我們必須談到三角學和角,因為弧度制是依託它們二者存在的。依據三角學在數學研究中的地位,筆者認為三角學的發展可以分為萌芽階段、傳播階段和確立階段三個階段。萌芽階段從公元前約300年古巴比倫時期開始到公元640年希臘古代數學落幕為止,這段時期由於天文學的需要,三角學受到學者們的重視,它是天文學的一部分;傳播階段從公元640年希臘古代數學落幕後到15世紀文藝復興開始前為止,這段時期三角學在不同地區傳播,雖然其研究內容本質與萌芽階段時相比沒有區別,但它逐漸脫離天文學,成為了數學的一個分支;確立階段是從文藝復興開始至今,在微積分等新興數學力量的崛起下,三角學逐漸成為了其他數學分支中的一部分,而在此期間,弧度製成為了度量角的主要單位。
18世紀以前,人們一直是用線段的長來定義三角函數的。弧度定義的提出,是數學家Roger Cotes在1714年提出的,作為一種對角度的描述,使得對三角函數的研究大為簡化。中學數學教科書中都把radian 譯作“弧度”。 1881年,學者哈爾斯特(G.B.Halsted)等用希臘字母ρ表示弧度的單位.1907年,學者包爾(G.N.Bauer)用r表示;1909年,學者霍爾(A.G.Hall)等又用R來表示,例如將單位弧度(角度制1°)寫成(π/180)rad,人們習慣把弧度的單位省略。
譯作“弧度”。 1881年,學者哈爾斯特(G.B.Halsted)等用希臘字母ρ表示弧度的單位.1907年,學者包爾(G.N.Bauer)用r表示;1909年,學者霍爾(A.G.Hall)等又用R來表示,例如將單位弧度(角度制1°)寫成(π/180)rad,人們習慣把弧度的單位省略。

弧度制
弧度制的基本思想是使圓半徑與圓周長有同一度量單位,然後用對應的弧長與圓半徑之比來度量角度,這一思想的雛型起源於印度。那麼半圓的弧長為π,此時的正弦值為0,就記為sinπ= 0,同理,1/4圓周的弧長為π/2,此時的正弦為1,記為sin(π/2)=1。從而確立了用π、π/2分別表示半圓及1/4圓弧所對的中心角。其它的角也可依此類推。
任意角:在任意一個角一邊所對應的射線情況下,逆時針旋轉所形成的角稱為正角;順時針轉動所形成的角稱為負角;射線未作任何旋轉,仍留在原來位置,那麼我們也把它看成一個角,叫做零角。這樣,就可以將角由優角、劣角擴展到任意角。
如果用弧度製表示,正角的弧度值是一個正值(正實數),負角的弧度值是一個負值(負實數),零角的弧度值是零。因此,弧度制能使角的集合與實數集合R存在一一對應關係:每一個角都對應唯一一個確定的實數。
弧度分:正角的弧度值是一個正量(正實數),負角的弧度值是一個負量(負實數),零角的弧度值是零。弧度制能使角的集合與實數集合R存在一一對應關係:每一個角都對應唯一的一個實數。
角度制,就是用角的大小來度量角的大小的方法。在角度制中,我們把周角的1/360看作1度,那麼,半周就是180度,一周就是360度。由於1度的大小不因為圓的大小而改變,所以角度大小是一個與圓的半徑無關的量。
弧度制,顧名思義,就是用弧的長度來度量角的大小的方法。單位弧度定義為圓周上長度等於半徑的圓弧與圓心構成的角。由於圓弧長短與圓半徑之比,不因為圓的大小而改變,所以弧度數也是一個與圓的半徑無關的量。角度以弧度給出時,通常不寫弧度單位,有時記為rad或R。
換算
一個完整的圓的弧度是2π,所以:
2π rad = 360°,1 π rad = 180°,1°=π/180° rad ,1 rad = (180/π)°≈57.30°=57°18ˊ
推導:由弧度定義得
推導:(角度制角度為n°)由,將α代入,得到
做圓周運動的物體在單位時間內所走的弧度即為角速度。符號:ω,單位:弧度每秒(rad/s)。定義公式:(α為所走過弧度,t為時間)。
由角速度、線速度(速率)的定義公式及弧長公式可以推出角速度與線速度的關係式:(r為半徑)
做周期運動的物體完成一次周而復始的運動所需的時間即為周期。符號:T,單位:秒(s)。
在勻速圓周運動中,周期T與角速度ω有關,關係式為。
弧度制之所以能成為當今數學主要的角的單位制度,主要原因有二:
(一)使進位制統一。在古巴比倫以及古希臘時期,數學家在研究天文學問題時,普遍習慣使用60進位對角進行度量,為了進位制的統一,也用60進位度量弦長和弧長。此時,角度制滿足了這種需求。而隨著歷史的發展,10進位取代了60進位成為了度量長度的主要進位制。為了保持進位制的統一,自然地也將角的進位制換成10進位。弧度制滿足了這一需求,而且可以與角度制進行一一對應的換算,與原有數學系統相容.這樣,在查閱三角函數表時就可以看到用統一進位製表示的數,便於數與數之間的對比,提高解決問題的效率。
(二)簡化微積分創立后公式的計算.弧度制大約直到18世紀才被提出來,它的提出是受到微積分等近代數學發展的推動的。在弧度制下,與三角函數有關的一些公式在形式上均比角度制下有很大的簡化。正是因為這樣的優越性,弧度制才逐漸被數學界普遍接受和廣泛使用。