勻變速直線運動
加速度不變的直線運動
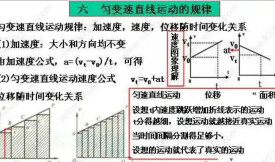
勻變速直線運動,速度均勻變化的直線運動,即加速度不變的直線運動。其速度時間圖像是一條傾斜的直線,表示在任意相等的時間內速度的變化量都相同,即速度(v)的變化量與對應時間(t)的變化量之比保持不變(加速度不變),這樣的運動是變速運動中最簡單的運動形式,叫做勻變速直線運動。
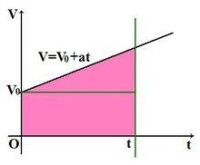
速度時間公式:
位移時間公式:;
速度位移公式:;
其中a為加速度,為初速度,為末速度,t為該過程所用時間,x為該過程中的位移。
V=V0+at
物體作勻變速直線運動須同時符合下述兩條:
(1)所受合外力不為零,且保持不變;
(2)合外力與初速度在同一直線上。
在勻變速直線運動中,如果物體的速度隨著時間均勻增加,這個運動叫做勻加速直線運動;如果物體的速度隨著時間均勻減小,這個運動叫做勻減速直線運動。
若速度方向與加速度方向相同(即同號),則是加速運動;若速度方向與加速度方向相反(即異號),則是減速運動。
一、位移公式推導:
(1)由於勻變速直線運動的速度是均勻變化的,故平均速度==中間時刻的瞬時速度
而勻變速直線運動的位移=平均速度×時間,故
利用位移公式和平均速度公式,得平均速度為
=
(2)利用微積分的基本定義可知,速度函數(關於時間)是位移函數的導數,而加速度函數是關於速度函數的導數,寫成式子就是,
於是,就是初速度,可以是任意的常數
進而有 ,(對於勻變速直線運動),顯然t=0時,s=0,故這個任意常數C=0,於是有
這就是位移公式。
(3)(代表相鄰相等時間段內位移差,T代表相鄰相等時間段的時間長度)
前一秒位移:
前兩秒位移:
可計算出,前兩秒位移之差為。此為從初速度為零的運動的推導,初速度不為零也可得到相同結論。
(4)
聯立位移公式和速度公式,即可證明之。
二、速度公式推導
(1)中間位移的速度
證明:由位移公式,用換x可得到,
得到
再把代入到上式,可得
整理開平方后,即得
(2)中間時刻的速度
證明記為★式,記為●式
●式+★式,整理可得
把代入中,得到
(1)重要比例關係
由,得。
由,得s∝,或t∝2。
由,得s∝,或。
(2)基本比例(當初速度為0的勻加速運動)
①第1秒末、第2秒末、……、第n秒末的速度之比
推導:
②前1秒內、前2秒內、……、前n秒內的位移之比
。
推導:
③第1個t內、第2個t內、……、第n個t內(相同時間內)的位移之比
推導:
④通過前1s、前2s、前3s……、前ns的位移所需時間之比
推導:,當位移等比例增大時,根號內的比值也等比例增大。
⑤通過第1個s、第2個s、第3個s、……、第n個s(通過連續相等的位移)所需時間之比
推導:
一、概念
物體只在重力的作用下從靜止開始下落的運動。
1、運動學特點:其大小、方向均不變。
2、受力特點:在真空中物體只受重力,或者在空氣中,物體所受空氣阻力很小,和物體重力相比可忽略。
3、運動性質:自由落體運動是初速度為零的勻加速直線運動。所以勻變速直線運動的所有規律和初速度為零的勻加速直線運動中的各種比例關係都可用於自由落體運動。
4、自由落體的加速度:在同一地點,一切物體在自由落體運動中的加速度都相同,這個加速度叫重力加速度,用g表示,地球上不同的緯度,g值不同。其方向為豎直向下。通常計算時取9.8粗略計算時,取10。
二、規律
自由落體運動是初速度為零,加速度為g的勻加速直線運動,其運動規律如下:
1、三個基本公式:;;
2、三個特殊公式:
(1)在連續相等的時間(T)內位移之差為一恆定值,即
(2)某段時間內中間時刻的瞬時速度等於這段時間內的平均速度,即
(3)某段位移中間位置的瞬時速度與這段位移的初、末速度的關係是
3、四個比例公式(參照上述比例關係)
物體具有豎直向上的初速度,加速度始終為重力加速度g的勻變速運動,可分為上拋時的勻減速運動和下落時的自由落體運動的兩過程。它是初速度為(不等於0)的勻減速直線運動與自由落體運動的合運動,運動過程中上升和下落兩過程所用的時間相等,只受重力作用且受力方向與初速度方向相反。
計算公式
(以方向為正方向):
(1)
(2)
(3)
(4)
(5)豎直上拋物體達到最大高度所需時間,可由速度公式和條件得到,即
註:也可以根據上升過程是,的勻變速直線運動,下落階段是自由落體運動來分析。