有向圖
圖論的基本研究對象
在數學上,一個圖(Graph)是表示物件與物件之間的關係的方法,是圖論的基本研究對象。一個圖看起來是由一些小圓點(稱為頂點或結點)和連結這些圓點的直線或曲線(稱為邊)組成的。如果給圖的每條邊規定一個方向,那麼得到的圖稱為有向圖,其邊也稱為有向邊。在有向圖中,與一個節點相關聯的邊有出邊和入邊之分,而與一個有向邊關聯的兩個點也有始點和終點之分。相反,邊沒有方向的圖稱為無向圖。
圖又有各種變體,包括簡單圖/多重圖;有向圖/無向圖等,但大體上有以下兩種定義方式。
圖G是一個二元組(V,E),其中V稱為頂點集,E稱為邊集。它們亦可寫成V(G)和E(G)。 E的元素是一個二元組數對,用(x,y)表示,其中。
一個圖,是指一個三元組(V,E,I),其中V稱為頂集(Vertices set),E稱為邊集(Edges set),E與G不相交;I稱為關聯函數,I將E中的每一個元素映射到。如果那麼稱邊e連接頂點u,v,而u,v則稱作e的端點,u,v此時關於e相鄰。同時,若兩條邊i,j有一個公共頂點u,則稱i,j關於u相鄰。
直觀來說,若圖中的每條邊都是有方向的,則稱為有向圖。有向圖中的邊是由兩個頂點組成的有序對,有序對通常用尖括弧表示,如表示一條有向邊,其中vi是邊的始點,vj是邊的終點。和代表兩條不同的有向邊。
【完全有向圖】
有n個頂點的有向圖有n(n-1)條邊,則此圖稱為完全有向圖。
在有 n個頂點的有向圖中,每個頂點的度最大可達 2(n-1)
如果給圖的每條邊規定一個方向,那麼得到的圖稱為有向圖,其邊也稱為有向邊。在有向圖中,與一個節點相關聯的邊有出邊和入邊之分,而與一個有向邊關聯的兩個點也有始點和終點之分。相反,邊沒有方向的圖稱為無向圖。
一個圖如果
若允許兩結點間的邊數多於一條,又允許頂點通過同一條邊和自己關聯,則為多重圖的概念。它只能用“三元組的定義”。
一個不帶權圖中若兩點不相鄰,鄰接矩陣相應位置為0,對帶權圖(網),相應位置為∞。一個圖的鄰接矩陣表示是唯一的,但其鄰接表表示不唯一。在鄰接表中,對圖中每個頂點建立一個單鏈表(並按建立的次序編號),第i個單鏈表中的結點表示依附於頂點vi的邊(對於有向圖是以頂點vi為尾的弧)。每個結點由兩個域組成:鄰接點域(Adjvex),用以指示與vi鄰接的點在圖中的位置,鏈域(Nextarc)用以指向依附於頂點vi的下一條邊所對應的結點。如果用鄰接表存放網(帶權圖)的信息,則還需要在結點中增加一個存放權值的域(Info)。每個頂點的單鏈表中結點的個數即為該頂點的出度(與該頂點連接的邊的總數)。無論是存儲圖或網,都需要在每個單鏈表前設一表頭結點,這些表頭結點的第一個域data用於存放結點vi的編號i,第二個域firstarc用於指向鏈表中第一個結點。
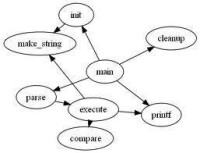
有向圖
深度優先搜索法是樹的先根遍歷的推廣,它的基本思想是:從圖G的某個頂點v0出發,訪問v0,然後選擇一個與v0相鄰且沒被訪問過的頂點vi訪問,再從vi出發選擇一個與vi相鄰且未被訪問的頂點vj進行訪問,依次繼續。如果當前被訪問過的頂點的所有鄰接頂點都已被訪問,則退回到已被訪問的頂點序列中最後一個擁有未被訪問的相鄰頂點的頂點w,從w出發按同樣的方法向前遍歷,直到圖中所有頂點都被訪問。
其遞歸演演算法如下:
Boolean visited[MAX_VERTEX_NUM]; //訪問標誌數組
Status (*VisitFunc)(int v); //VisitFunc是訪問函數,對圖的每個頂點調用該函數
void DFSTraverse (Graph G, Status(*Visit)(int v)){
VisitFunc = Visit;
for(v=0; v
visited[v] = FALSE; //訪問標誌數組初始化
for(v=0; v
if(!visited[v])
DFS(G, v); //對尚未訪問的頂點調用DFS
}
void DFS(Graph G, int v){ //從第v個頂點出發遞歸地深度優先遍歷圖G
visited[v]=TRUE; VisitFunc(v); //訪問第v個頂點
for(w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w))
//FirstAdjVex返回v的第一個鄰接頂點,若頂點在G中沒有鄰接頂點,則返回空(0),//若w是v的鄰接頂點,NextAdjVex返回v的(相對於w的)下一個鄰接頂點。
//若w是v的最後一個鄰接點,則返回空(0)。
if(!visited[w])
DFS(G, w); //對v的尚未訪問的鄰接頂點w調用DFS
}
圖的廣度優先搜索是樹的按層次遍歷的推廣,它的基本思想是:首先訪問初始點vi,並將其標記為已訪問過,接著訪問vi的所有未被訪問過的鄰接點vi1,vi2,…, vi t,並均標記已訪問過,然後再按照vi1,vi2,…, vi t的次序,訪問每一個頂點的所有未被訪問過的鄰接點,並均標記為已訪問過,依次類推,直到圖中所有和初始點vi有路徑相通的頂點都被訪問過為止。其非遞歸演演算法如下:
Boolean visited[MAX_VERTEX_NUM]; //訪問標誌數組
Status (*VisitFunc)(int v); //VisitFunc是訪問函數,對圖的每個頂點調用該函數
void BFSTraverse (Graph G, Status(*Visit)(int v)){
VisitFunc = Visit;
for(v=0; v
visited[v] = FALSE;
initQueue(Q); //置空輔助隊列Q
for(v=0; v
if(!visited[v]){
visited[v]=TRUE; VisitFunc(v);
EnQueue(Q, v); //v入隊列
while(!QueueEmpty(Q)){
DeQueue(Q, u); //隊頭元素出隊並置為u
for(w=FirstAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w))
if(!Visited[w]){ //w為u的尚未訪問的鄰接頂點
Visited[w]=TRUE; VisitFunc(w);
EnQueue(Q, w);
}
}
}
}