定點小數
定點小數
定點小數是計算機處理的數值數據多數帶有小數,小數點在計算機中通常有兩種表示方法,一種是約定所有數值數據的小數點隱含在某一個固定位置上,稱為定點表示法,簡稱定點數
8位字長純小數,第一位為符號位,小數點在第一位後面,后七位為具體數值,如:-0.1001原碼錶示為1.1001,反碼為1.0110,補碼為1.0111-1的補碼為1.0000000
.示(fixed-point)
謂式,即約器據置固。計算采簡單約:置固據,固低。般稱,整。
是純小數,約定的小數點位置在符號位之後、有效數值部分最高位之前。若數據x的形式為x=x.xx…x(其中x為符號位,x~x是數值的有效部分,也稱為尾數,x為最高有效位),則在計算機中的表示形式為:
一般說來,如果最末位x=1,前面各位都為0,則數的絕對值最小,即|x|=2^(-n)。如果各位均為1,則數的絕對值最大,即|x|=1-2^(-n)。所以定點小數的表示範圍是:
2^(-n)≤|x|≤1-2^(-n)
由於“編碼總位數為8”的限制,真值-128無法用原碼、反碼來表示,似乎不能用上述規則來求解補碼,但實際上是可行的——只要不管它的最高位即可,操作辦法如下:
將128化為二進位為:10000000,最高位為1,可以只對捨去最高位后剩餘的7位進行處理即可,首先取反得:1111111,加1得:10000000,最高位有進位需丟棄,即得:0000000,加上符號位就得補碼:10000000。
又如,當編碼總位數為4時,真值X=+0.101的原碼、反碼、補碼均為:0101。
真值X=-0.101的原碼、反碼、補碼依次為:1101、1010、1011。
同理,特例,-1的補碼為:1000。
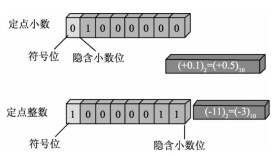
在定點小數中,小數點隱含在第一位編碼和第二位編碼之間
定點小數,是指小數點準確固定在數據某個位置上的小數,從實用角度看,都把小數點固定在最高數據位的左邊,小數點前邊再設一位符號位。按此規則,任何一個小數都可以被寫成:
N=NS.NN…N
如果在計算機中用m+1個二進位位表示上述小數,則可以用最高(最左)一個二進位位表示符號(如用0表示正號,則1就表示負號),而用後面的m個二進位位表示該小數的數值。小數點不用明確表示出來,因為它總是固定在符號位與最高數值位之間,已成定論。定點小數的取值範圍很小,對用m+1個二進位位的小數來說,其值的範圍為:
|N|≤1-2^(-m)即小於1的純小數,這對用戶算題是十分不方便的,因為在算題前,必須把要用的數,通過合適的"比例因子"化成絕對值小於1的小數,並保證運算的中間和最終結果的絕對值也都小於1,在輸出真正結果時,還要把計算的結果按相應比例加以擴大。
定點小數表示法,主要用在早期的計算機中,它最節省硬體。隨著計算機硬體成本的大幅度降低,現代的通用計算機都被設計成能處理與計算多種類型數值的計算機。我們將主要通過定點小數討論數值數據的不同編碼方案,而且,定點小數也被用來表示浮點數的尾數部分。