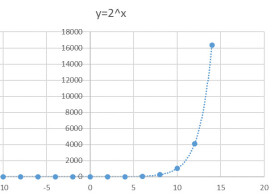
指數爆炸
指數函數的爆炸性增長
指數爆炸的概念:即指數函數的“爆炸性”增長(blow up)。
指數的概念:在乘方a中,其中的a叫做底數,n叫做指數,結果叫冪。
f(x)=a^x (a為常數,如圖中a=2 x為指數) 隨著x單位長度的遞增,f(x)會呈“爆炸性”增長
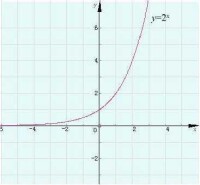
指數函數y=2^x的圖像
x2=1 f(x2)=2
x3=2 f(x3)=4
x4=3 f(x4)=8
x5=4 f(x5)=16
x6=5 f(x6)=32
x7=6 f(x7)=64
·· ····
·· ····
·· ····
x21=20 f(x21)=1048576
一張紙對摺一次,厚度變成原來的2倍。
再對摺第二次,變為原來的2的2次方倍即4倍。
以此類推,假設紙的厚度為0.1mm,則對摺24次以後,長度超過1千米;對摺39次達55000千米,超過地球赤道長度;對摺42次達44萬千米,超過地球至月球的距離;對摺51次達22億千米,超過地球至太陽的距離;對摺82次為51113光年,超過銀河系半徑的長度。不過,只是一個不符合實際的數學理論推理數字。
那麼在現實生活中,一張紙究竟能折多少次呢?
如果紙為正方形,邊長為a,厚度為h,當摺疊一次的時候,摺疊邊長不變,厚度為2倍的h,摺疊兩次的時候,摺疊邊長為原邊長的二分之一,厚度變為4倍的h,就這樣摺疊下去,可以推出一個公式:當摺疊次數n為偶數次時,摺疊邊長為l/(2^(0.5*n)),厚度變為2^n*h,當滿足n>2/3*(log2(l/h)-1)時無法摺疊。根據一般的紙張的狀況,厚度大約為0.1mm,邊長為1m時,根據以上公式,可以得出n>8.1918時無法摺疊,這意味著對於厚度大約為0.1mm,邊長為1m的正方形紙,只能摺疊8次。但8次人類是很難辦到的,只能依靠機器。
所以,一張紙最多能對摺多少次實際是一個變數,它取決於紙張的實際厚度與大小。
在現實生活中,一張普通的A4紙,一般人可以折到6次,厲害的人可以折到7次。
傑米是百萬富翁。一天,他碰到上一件奇怪的事。一個叫韋伯的人對他說:“我想和你訂個合同,我將在整整一個月中每天給你10萬元,而你第一天只需給我1分錢,以後你每天給我的錢是前一天的兩倍。”傑米說:“真的?!你說話算數?”
合同開始生效了,傑米欣喜若狂。第一天傑米支出1分錢,收入10萬元。第二天,傑米支出2分錢,收入10萬元。到了第10天,傑米共得100萬元,而總共才付出5元1角2分。到了第20天,傑米共得200萬元,而韋伯才得5千元多。傑米想:要是合同訂二、三個月該多好!可從21天起,情況發生了轉變。
第21天傑米支出1萬多,收入10萬。到第28天,傑米支出134萬多,收入10萬。結果,傑米在一個月(31天)內得到310萬元的同時,共付給韋伯2千1百多萬元!傑米破產了。
指數爆炸