指數函數

指數函數

指數函數是重要的基本初等函數之一。一般地，y=a^x函數(a為常數且以a>0，a≠1)叫做指數函數，函數的定義域是 R 。

目錄

1基本概念 2數學術語 3基本性質

4運演算法則 5函數圖像 6冪的比較

基本概念

細胞的分裂是一個很有趣的現象，新細胞產生的速度之快是十分驚人的。例如某種細胞在分裂時，1個分裂成2個，2個分裂成4個……第x次分裂得到新細胞數y與分裂次數x的函數關係式：。

這個函數是冪的形式，且自變數為冪指數，我們下面來研究這樣的函數。

一般地，函數 (a為常數且以a>0，a≠1)叫做指數函數，函數的定義域是R。對於一切指數函數來講，值域為(0， +∞)。

指數函數中前面的係數為1。如：都是指數函數；不是指數函數。

數學術語

指數函數是數學中重要的函數。應用到值e上的這個函數寫為exp(x)。還可以等價地寫為e，這裡的e是數學常數，就是自然對數的底數，近似等於 2.718281828，還稱為歐拉數。

當a>1時，指數函數對於x的負數值非常平坦，對於x的正數值迅速攀升，在 x等於0的時候，y等於1。當0

作為實數變數x的函數，的圖像總是正的(在x軸之上)並遞增(從左向右看)。它永不觸及x軸，儘管它可以無限程度地靠近x軸(所以，x軸是這個圖像的水平漸近線。它的反函數是自然對數ln(x)，它定義在所有正數x上。

有時，尤其是在科學中，術語指數函數更一般性地用於形如（k屬於R）的函數，這裡的 a 叫做“底數”，是不等於 1 的任何正實數。本文最初集中於帶有底數為歐拉數e 的指數函數。

指數函數的一般形式為 (a>0且≠1) (x∈R)，從上面我們關於冪函數的討論就可以知道，要想使得x能夠取整個實數集合為定義域，則只有使得a>0且a≠1。

基本性質

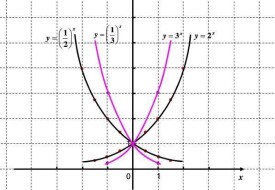
如圖所示為a的不同大小影響函數圖形的情況。

在函數中可以看到：

（1）指數函數的定義域為R，這裡的前提是a大於0且不等於1。對於a不大於0的情況，則必然使得函數的定義域不連續，因此我們不予考慮，同時a等於0函數無意義一般也不考慮。

（2）指數函數的值域為(0， +∞)。

（3）函數圖形都是上凹的。

（4） a>1時，則指數函數單調遞增；若0

（5）可以看到一個顯然的規律，就是當a從0趨向於無窮大的過程中（不等於0）函數的曲線從分別接近於Y軸與X軸的正半軸的單調遞減函數的位置，趨向分別接近於Y軸的正半軸與X軸的負半軸的單調遞增函數的位置。其中水平直線y=1是從遞減到遞增的一個過渡位置。

（6）函數總是在某一個方向上無限趨向於X軸，並且永不相交。

（7）函數總是通過（0，1）這點,(若 ,則函數定過點(0,1+b))

（8）指數函數無界。

（9）指數函數是非奇非偶函數

（10）指數函數具有反函數，其反函數是對數函數，它是一個多值函數。

運演演算法則

徠①

②

③

④

函數圖像

(1)由指數函數y=a^x與直線x=1相交於點（1，a)可知：在y軸右側，圖像從下到上相應的底數由小變大。

(2)由指數函數y=a^x與直線x=-1相交於點（-1，1/a）可知：在y軸左側，圖像從下到上相應的底數由大變小。

(3)指數函數的底數與圖像間的關係可概括的記憶為：在y軸右邊“底大圖高”；在y軸左邊“底大圖低”。（如右圖）。

(4) 與的圖像關於y軸對稱。

冪的比較

比較大小常用方法：

（1）做差（商）法：A-B大於0即A大於B A-B等於0即A=B A-B小於0即A小於B 步驟：做差—變形—定號—下結論；A\B大於1即A大於B A\B等於1即A等於B A/B小於1即A小於B （A，B大於0）

（2）函數單調性法；

（3）中間值法：要比較A與B的大小，先找一個中間值C，再比較A與C、B與C的大小，由不等式的傳遞性得到A與B之間的大小。

比較兩個冪的大小時，除了上述一般方法之外，還應注意：

（1）對於底數相同，指數不同的兩個冪的大小比較，可以利用指數函數的單調性來判斷。

例如：y1=3 ，y2=3 因為3大於1所以函數單調遞增（即x的值越大，對應的y值越大），因為5大於4，所以y2 大於y1 。

（2）對於底數不同，指數相同的兩個冪的大小比較，可以利用指數函數圖像的變化規律來判斷。

例如： , ,因為1/2小於1所以函數圖像在定義域上單調遞減；3大於1，所以函數圖像在定義域上單調遞增，在x=0是兩個函數圖像都過（0，1）然後隨著x的增大，y1圖像下降，而y2上升，在x等於4時，y2大於y1.

（3）對於底數不同，且指數也不同的冪的大小比較，則可以利用中間值來比較。如：

<1> 對於三個（或三個以上）的數的大小比較，則應該先根據值的大小（特別是與0、1的大小）進行分組，再比較各組數的大小即可。

<2> 在比較兩個冪的大小時，如果能充分利用“1”來搭“橋”（即比較它們與“1”的大小），就可以快速地得到答案。那麼如何判斷一個冪與“1”大小呢？由指數函數的圖像和性質可知“同大異小”。即當底數a和1與指數x與0之間的不等號同向（例如： a 〉1且x 〉0，或0〈 a〈 1且 x〈 0）時，大於1，異向時小於1。

目錄