緩和曲線
緩和曲線
緩和曲線指的是平麵線形中,在直線與圓曲線、圓曲線與圓曲線之間設置的曲率連續變化的曲線。緩和曲線是道路平麵線形要素之一,它是設置在直線與圓曲線之間或半徑相差較大的兩個轉向相同的圓曲線之間的一種曲率連續變化的曲線。《公路工程技術標準》(JTG B01-2003)規定,除四級路可不設緩和曲線外,其餘各級公路都應設置緩和曲線。在現代高速公路上,有時緩和曲線所佔的比例超過了直線和圓曲線,成為平麵線形的主要組成部分。在城市道路上,緩和曲線也被廣泛地使用。
緩和曲線的作用:
1、緩和曲率——使曲率連續變化;
2、緩和超高——使橫向坡度連續變化;
3、緩和加寬——使車道加寬連續變化。
緩和曲線產生的效果:
1、曲率連續變化,便於車輛駕駛;
2、離心加速度連續變化,沒有突變,乘客感覺舒適;
3、超高橫坡度及加寬逐漸變化,行車更加穩定;
4、與圓曲線配合,增加線形美觀。
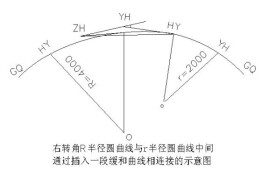
由於直線與圓曲線間存在曲率半徑的突變,圓曲線半徑越大,這種突變程度就越小。當圓曲線半徑超過2000m時,這種突變對軌道交通行車影響很小。而當正線上曲線半徑不大於2000m時,則要在圓曲線與直線間加設緩和曲線,實現曲率半徑的逐漸過渡,減少列車在突變點處的輪軌衝擊。因此,《地鐵設計規範》(GB50157—2003)規定:“線路平面圓曲線與直線之間應根據曲線半徑、超高設置及設計速度等因素設置緩和曲線,其長度可按表的規定採用。”
地鐵緩和曲線長度
| R/L/.V | 100 | 95 | 90 | 85 | 80 | 75 | 70 | 65 | 60 | 55 | 50 | 45 | 40 | 35 | 30 |
| 3000 | 30 | 25 | 20 | ||||||||||||
| 2500 | 35 | 30 | 25 | 20 | |||||||||||
| 2000 | 40 | 35 | 30 | 25 | 20 | 20 | |||||||||
| 1500 | 55 | 50 | 45 | 35 | 30 | 25 | 20 | ||||||||
| 1200 | 70 | 60 | 50 | 40 | 35 | 30 | 25 | 20 | 20 | ||||||
| 1000 | 85 | 70 | 60 | 50 | 45 | 35 | 30 | 25 | 25 | ||||||
| 800 | 85 | 80 | 75 | 65 | 55 | 45 | 40 | 35 | 30 | 25 | 20 | ||||
| 700 | 85 | 80 | 75 | 70 | 60 | 50 | 45 | 35 | 30 | 25 | 20 | 20 | |||
| 650 | 85 | 80 | 75 | 70 | 60 | 55 | 45 | 40 | 35 | 30 | 25 | 20 | 20 | ||
| 600 | 85 | 75 | 70 | 70 | 60 | 50 | 45 | 35 | 30 | 20 | 20 | 20 | |||
| 550 | 75 | 70 | 70 | 65 | 55 | 45 | 40 | 35 | 20 | 20 | 20 | ||||
| 500 | 70 | 70 | 65 | 60 | 50 | 45 | 35 | 20 | 20 | 20 | 20 | ||||
| 450 | 70 | 65 | 60 | 55 | 50 | 40 | 25 | 20 | 20 | 20 | |||||
| 400 | 65 | 60 | 60 | 55 | 45 | 25 | 20 | 20 | 20 | ||||||
| 350 | 60 | 60 | 60 | 35 | 30 | 25 | 20 | 20 | 20 | ||||||
| 300 | 60 | 60 | 60 | 35 | 30 | 25 | 20 | 20 | |||||||
| 250 | 60 | 60 | 40 | 35 | 30 | 20 | 20 | ||||||||
| 200 | 60 | 40 | 40 | 35 | 25 | 20 | |||||||||
| 150 | 40 | 40 | 35 | 25 |
緩和曲線的線型多種多樣,如迴旋線、三次拋物線、七次四項式型、半波正弦型、一波正弦型、雙紐線、多心復曲線……
我國常用的線型有兩種:三次拋物線、迴旋線。其中三次拋物線是迴旋線的近似結果。
鐵路上常用的緩和曲線是三次拋物線型。其方程式為:
上式中C是三次拋物線參數,它越大緩和曲線越緩。它近似的等於圓曲線半徑乘以緩和曲線長度,即
三次拋物線型緩和曲線的優點是鋪設和養護維修比較容易,緩和曲線長度比較短;其缺點是始、終點存在折角,影響行車的平穩性。
公路、匝道常用的緩和曲線是迴旋線,也叫放射螺旋線。迴旋線不僅線形美觀,而且與駕駛員勻速轉動方向盤由圓曲線駛入直線或者由直線駛入圓曲線的軌跡線相符合。
迴旋線的本質特徵是:
即曲率k隨弧長l線性變化;
表示曲率隨弧長的增大而增大或減小;
是迴旋線參數。它是圓曲線半徑 R 與緩和曲線全長的幾何平均值,單位為米。對於一條緩和曲線而言,它是一個常數。A 越大,說明曲率變化越慢,曲線拐彎越緩;A越小,說明曲率變換越快,曲線拐彎越急。
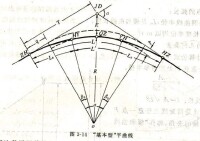
實地放樣緩和曲線之前,需要計算若干曲線要素:
緩和曲線
不同類型的緩和曲線,數值不同
p不同類型的緩和曲線,數值不同
q不同類型的緩和曲線,數值不同
上面的公式中
——路線偏轉角,單位:弧度。這是設計數據;
R——圓曲線半徑,單位:m。這是設計數據;
——緩和曲線偏轉角,單位:弧度;
p——內移距,單位:m;
q——切線增長,單位:m;(有些文獻用 m 表示該變數)
T——切線長,單位:m;
E——外距,單位:m;
D——切曲差,即切線長減去曲線長,單位:m;
注意:的計算公式請見下文,每種類型的緩和曲線都有自己的計算公式。
[式中為路線設計參數,R值對於設計道路可查相關規範 ]
迴旋線最本質的特點就是
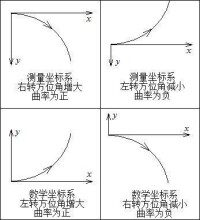
為了確定上式的正負號,需要對曲率的正負號取值做個約定
數學上曲率的定義為,即曲率是前進方位角T隨弧長l的變化率。
在的情況下,若則k取正值,若則k取負值。
下圖分四種情況,對曲率的正負號取法進行了說明:
曲率的正負號取法
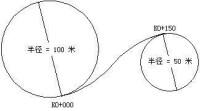
公式中,參數A無法反映出曲率隨弧長增大,到底是增大還是減小?為此引入常量a,它滿足下式
a就是曲率變化率,它可能是正數,也可能是負數。
a與A的關係滿足公式
為了說明a的符號,以及它與A的關係,請見下圖
a的符號與A的關係
曲率變化率 參數
在數學坐標系下K0+000處的曲率為(左轉為正),K0+150處的曲率為(右轉為負)。可知:
曲率變化率參數
求解微分方程 可得
曲率k隨樁號L變化的函數為。當時
前進方向T隨樁號L變化的函數為。當 時
坐標隨樁號L變化的函數為(用到了複數):
當時
特別的,當時
當時,令,則
這個特解與通解相比,簡化了不少。它的含義其實就是在曲率為零的地方建立坐標系。如下圖所示,在直緩點建立了坐標系:
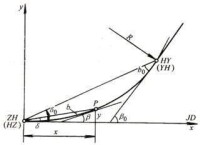
緩和曲線
從原點開始沿迴旋線行走距離,到達點P,其坐標為(x,y)。
點 P 處的切線與軸夾角為,稱其為切線角,也是點 P 處的前進方位角。
原點與點 P 的連線叫弦,其長度為c,也就是弦長。
原點到點 P 的方位角為,也就是偏角,也叫弦切角。
點 P 處,切線與弦線的夾角為
從原點開始沿迴旋線行走距離,到達緩圓點HY,即迴旋線的長度為
圓曲線的半徑為R
在緩圓點處達到最大值
接下來,計算各個參數:
曲率變化率
參數
曲率
曲率半徑
切線角
最大切線角
坐標
弦長的計算公式如下:
弦切角的計算公式如下:
注意:亦即弦切角近似的等於切線角的三分之一。
迴旋線的曲線要素計算公式如下:
迴旋曲線段,根據樁號 L,距中 Z,計算前進方向 T 及坐標 x,y的公式如下:
上式需要一個起算點,即需要知道樁號處的 。也可以從曲率為零的點開始起算,根據可知:當時曲率為零。是迴旋線上任意一點的樁號和曲率。
距中 Z 的正方向是前進方向 T 加上,因此:
在數學坐標系下,距中 Z 左正右負,即在迴旋線沿樁號增加方向右側取負值;
在測量坐標系下,距中 Z 左負右正,即在迴旋線沿樁號增加方向左側取負值。
參數 C 按下式計算:
更高次項的係數,請見下表
1 2/5 1123/3600 23519/78000 93134377/286416000 671176607/1790100000 60632952362431/134042688000000 10959451729410359/19436189760000000 28568328624908898433/39649827110400000000 596762934176757576209/635718894670080000000 2098157146254959366777509639/1688977959359468544000000000 14062585980252142453129239257/8444889796797342720000000000 3127534025901397259312263980851/1386126739060529356800000000000 |
上式中,R 是圓曲線的曲率半徑。它是有正負號的,具體取法請參考前文;是緩和曲線長度,注意它也是有正負號的:順著前進方向為正,逆著前進方向為負。現舉例說明,如下圖所示
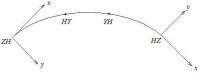
緩和曲線
以HZ點為原點的坐標系是數學坐標系,將根據 YH 點計算C。從 YH 至 HZ(樁號增加的方向)右轉,因此YH處的曲率半徑 R 取負值。YH 點的樁號比 HZ 點的樁號小,所以 Ls 也取負值。最終 C 為正值。
注意:使用上述規則時,要求x 軸必須是切線,而且其正方向是樁號增加的方向。
更為一般的計算公式為:
上式中:是三次拋物線上任意一點的曲率半徑,是該點的樁號減去曲率為零點的樁號。
坐標 x 按下式計算
更高次項的係數,請見下表
1 -1/40 23/5760 -2773/2995200 2066579/8146944000 -224209943/2932899840000 28747533091/1173159936000000 -261175434475093/31844253302784000000 86647036511116753/30570483170672640000000 -2316511336548771758119/2307460069722370867200000000 35677500215657115786212861/98390097372961893777408000000000 |
坐標y 按下式計算
更高次項的係數,請見下表
1/6 -1/80 133/57600 -16933/29952000 23345441/146644992000 -95319797/1955266560000 13001597946211/823558275072000000 -1694382133343581/318442533027840000000 9603494098034819239/5196982139014348800000000 |
曲率按下式計算:
更高次項的係數,請見下表
1 -2/5 121/720 -3337/46800 1932763/63648000 -579833/44752500 1585042411/286416000000 -9194722916339/3887237952000000 943636378388861/932937108480000000 -1904209296741873383/4401130809254400000000 69481023021498242079629/375328435413215232000000000 -11534698506084794283343/145601548220643840000000000 16035089603343026034099263/472913828620651192320000000000 |
曲率半徑等於曲率的倒數
切線角按下式計算:
更高次項的係數,請見下表
1/2 -1/15 121/7200 -3337/655200 1932763/1145664000 -579833/984555000 1585042411/7446816000000 -9194722916339/116617138560000000 943636378388861/31719861688320000000 -1904209296741873383/167242970751667200000000 69481023021498242079629/15763794287355039744000000000 -11534698506084794283343/6697671218149616640000000000 16035089603343026034099263/23645691431032559616000000000000 |
最大切線角按下式計算
更高次項的係數,請見下表
1/2 2/15 167/1800 46351/546000 25385099/286416000 5252428289/52509600000 3982854295663/33510672000000 4270501632677849/29154284640000000 7356042227375864101/39649827110400000000 11595993887859194946607/48314635994926080000000 1866776187030795889021687763/5911422857758139904000000000 233123111824877589842938537/553368847083586560000000000 114262828881514570894054876308869 /200988377163776756736000000000000 |
弦長按下式計算
更高次項的係數,請見下表
1 -1/90 7/3240 -1021/1895400 -103137467/148478054400 1824489697/267260497920000 1962656897729/320712597504000000 172597317854624597/17410845493297152000000 12570996329063196101/12535808755173949440000000 -84559611892561668247007/73412289685903166668800000000 986086453888432129684636273/2402965612958834641128652800000000 |
弦切角按下式計算:
更高次項的係數,請見下表
1/6 -4/405 329/194400 -279619937/50948352000 49981690783/400890746880000 -10875344672639/352783857254400000 112198229967587/11545653510144000000 -142446483534146625839/18803713132760924160000000 52613217024783269917249/38359574790832285286400000000 3424580749757991824764543627/15532865900902135616451379200000000 -1413931320131094500306391029838659/32941774994930072328304475504640000000000 |
最大弦切角按下式計算
更高次項的係數,請見下表
1/6 23/405 2033/48600 1740762847/50948352000 10960255204399/400890746880000 6772270615585369/352783857254400000 1193239078444885151/150093495631872000000 -161805233310981385370591/18803713132760924160000000 -1286980164945796856981760287/38359574790832285286400000000 -72056068243648037753159483098122901/1009636283558638815069339648000000000 -4238353071056815709683515980381542179491/32941774994930072328304475504640000000000 -562636180723418426132797552941934630463/2614426586899212089547974246400000000000 -232168897210836372569220251035298614709587903/672012209896573475497411300294656000000000000 |
更高次項的係數,請見下表
1/24 -19/1920 -9139/691200 -3240559/159744000 -282589603597/8798699520000 -7026310366847/140779192320000 -19235406274658191/253402546176000000 -1157743059288068176933/10190161056890880000000 -31472972322721395868013113/187091357004516556800000000 -593565174736535737082257554883/2399758472511265701888000000000 -2404682875032206089252747022332201/6641331572674927829975040000000000 -1872334767018224961225647555546981/3542043505426628175986688000000000 |
更高次項的係數,請見下表
1/2 -11/80 -5321/57600 -52487/7488000 18677834707/146644992000 3188362247677/9776332800000 169430712200037851/274519425024000000 332286113603292440329/318442533027840000000 8671309730283052493037077/5196982139014348800000000 912479043985584874133797609/352905657722244956160000000 696256490101343458284600171876781/177102175271331408799334400000000 13074672153106612908209529164613637/2213777190891642609991680000000000 463819829160454637226871854554498260583/52687897143221094117801984000000000000 |