范德華方程
1873年提出的氣體狀態方程
范德華方程常用的形式()
在一般形式的范氏方程中,常數a和b 因氣體/流體種類而異,但我們可以通過改變方程的形式,得到一種適用於所有氣體/流體的普適形式。
按照下面的方式定義約減變數(亦稱摺合變數,就是把變數轉換成其無量綱形式),其中下標R 表示約減變數,下標C 表示原變數的臨界值:
用約減變數代替原變數,范氏方程形式變為如圖所示
這就是范氏方程的不變形式,即這一形式不會因應用流體種類改變而改變。
上述方程的不變性質亦稱對應態原理
范氏方程對氣-液臨界溫度以上流體性質的描寫優於理想氣體方程。對溫度稍低於臨界溫度的液體和低壓氣體也有較合理的描述。
但是,當描述對象處於狀態參量空間中氣液相變區(即正在發生氣液轉變)時,對於固定的溫度,氣相的壓強恆為所在溫度下的飽和蒸氣壓,即不再隨體積V(嚴格地說應該是單位質量氣體佔用的體積,即比容)變化而變化,所以這種情況下范氏方程不再適用。
在氣體壓強不太高的情況下,以下事實成立:
排斥體積b 的影響相對V 而言極小,可以忽略;以二氧化碳()為例,在標準狀況(,1標準大氣壓)下,一摩爾體積V 為,而相應的,比V 小3個數量級;
分子間的距離足夠大, 項完全可以視為0;譬如在一大氣壓下二氧化碳氣體的 值只有7‰。
所以此時理想氣體方程是范氏方程(也是對實際氣體行為的)的一個良好近似。
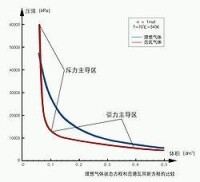
分別用理想氣體方程和范德瓦耳斯方程模擬的二氧化碳氣體70°C時的p-V等溫線
隨著氣體壓力的增加,范氏方程和理想氣體方程結果的差別會變得十分明顯(左圖為 分別用理想氣體方程和范德瓦耳斯方程模擬的p-V等溫線,溫度 ):
在壓強為(50~150標準大氣壓)的中壓區,由於體積被“壓小”導致分子間距靠近,分子間的引力(表現為 項)變得不可忽略。 項的存在使得氣體的壓強比不考慮分子間引力的理想氣體模型估計結果要小(所以左圖的中壓區里紅線比藍線要低)。
在壓強為15000kPa以上的高壓區,體積的急劇壓縮致使b 的影響不可忽略,於是范氏方程中的體積項(或比容項)將比理想氣體方程中的體積項要小(或者說:對應相同體積/比容值的壓強項會升高)。這一效應導致在高壓區范氏氣體的狀態線重新趕上並超過理想氣體線(見左圖的左上角)。
范氏方程適用於氣體的液化過程。氣體液化可能發生的最高溫度稱為臨界溫度,用表示:
當溫度時,無論給氣體施加多大的壓強都無法將它液化;
當溫度T
用范德瓦耳斯方程模擬的二氧化碳氣體不同溫度下壓縮過程的p-V等溫線,在臨界溫度以下時能看見明顯的液化過程右圖所示為用范氏方程模擬的 在不同溫度下的p-V 等溫線,從中可以明顯看出范氏方程對液化過程的模擬(注意:若用理想氣體狀態方程作上述模擬,得到的只是一系列雙曲線,因為在等溫條件下理想氣體狀態方程就退化為玻意耳-馬略特定律——)。 氣體的臨界溫度為。
時的曲線(右圖中藍線)形狀仍與玻義耳定律的結果(雙曲線)類似,儘管位置要略低;
當溫度下降到,曲線(右圖中右二的曲線)形狀發生明顯的變化,表現為兩個拐點的出現。但此時二氧化碳仍然以氣態存在;
溫度進一步降至臨界溫度(圖中紅線),若此時氣體受壓至體積小於某定值(隨溫度變化而變化),則氣體將發生液化。圖中 時曲線對應氣態 的p,V 值,V圖中13°C 和 21°C 對應的曲線只有兩拐點以外的部分是與物理實際相符的。當氣體被進一步壓縮至比右拐點對應體積更小時,氣體將進入液化區,在液化過程中實際氣體的線應是一段“平台”,而不是如圖所示的“駝峰”型。但完全液化后,液態的壓強卻仍能被圖中曲線恰當地反映,此時曲線隨體積的減小而劇烈上升,這一定程度上反映了液體的不可壓縮性。另外,我們從圖中能得到的另一個信息就是“液化平台”的長度隨溫度的下降而增加;
氣體的臨界狀態參量和范德瓦爾斯常數a、b之間存在下列數學關係:
我們可以利用這些關係通過測出氣體的和對應的來得到a 和b 的值(由於測量上的困難,一般不使用)。