理想氣體狀態方程
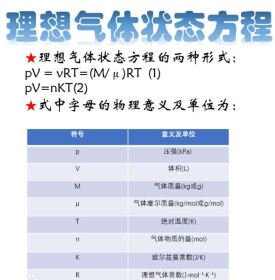
理想氣體狀態方程
理想氣體狀態方程，又稱理想氣體定律、普適氣體定律，是描述理想氣體在處於平衡態時，壓強、體積、物質的量、溫度間關係的狀態方程。它建立在玻義耳-馬略特定律、查理定律、蓋-呂薩克定律等經驗定律上。其方程為pV=nRT。這個方程有4個變數：p是指理想氣體的壓強，V為理想氣體的體積，n表示氣體物質的量，而T則表示理想氣體的熱力學溫度；還有一個常量：R為理想氣體常數。可以看出，此方程的變數很多。因此此方程以其變數多、適用範圍廣而著稱，對常溫常壓下的空氣也近似地適用。值得注意的是，把理想氣體方程和克拉伯龍方程等效是不正確的。一般克拉伯龍方程是指描述相平衡的方程dp/dT=L/(TΔv)。儘管理想氣體定律是由克拉伯龍發現，但是國際上不把理想氣體狀態方程叫克拉伯龍方程。
理想氣體狀態方程演示儀
平衡態的英文是equilibrium state。在不受外界影響的條件下，系統的宏觀性質不隨時間改變的狀態，稱為平衡態。處於平衡態的氣體分子仍在做熱運動，但系統的宏觀量不隨時間改變，是一種動態平衡。
由大量分子組成的物體叫作熱力學系統，簡稱系統，系統以外的物體統稱外界。
描述體系整體性質的物理量。例如壓強、溫度、體積。
描寫體系中每個粒子微觀運動狀態的物理量，例如質量、位置、速度。
公式如圖示。
其中M 為氣體的質量， μ為氣體的摩爾質量，R＝8.31J/（mol·K）為氣體的普適常數。上式可作為理想氣體的定義式。該式還可表示如圖示二。
其中n—分子數密度，即單位體積的分子數，—玻耳茲曼常數（Boltzman constant）。
理想氣體狀態方程是描述氣體宏觀運動的經驗規律。
理想氣體狀態方程
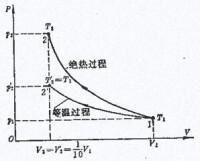
當n，T一定時 V，p成反比，即V∝（1/p）① （2）查理定律
當n，V一定時 p，T成正比，即p∝T ② （3）蓋-呂薩克定律
當n，p一定時 V，T成正比，即V∝T ③ （4）阿伏伽德羅定律
當T，p一定時 V，n成正比，即V∝n ④
由①②③④得
V∝（nT/p） ⑤
將⑤加上比例係數R得
V=（nRT）/p 即PV=nRT
實際氣體中的問題當理想氣體狀態方程運用於實際氣體時會有所偏差，因為理想氣體的基本假設在實際氣體中並不成立。如實驗測定1 mol乙炔在20℃、101kPa時，體積為24.1 dm，，而同樣在20℃時，在842 kPa下，體積為0.114 dm，，它們相差很多，這是因為，它不是理想氣體所致。
一般來說，沸點低的氣體在較高的溫度和較低的壓力時，更接近理想氣體，如氧氣的沸點為-183℃、氫氣沸點為-253℃，它們在常溫常壓下摩爾體積與理想值僅相差0.1%左右，而二氧化硫的沸點為-10℃，在常溫常壓下摩爾體積與理想值的相差達到了2.4%。
應用一定量處於平衡態的氣體，其狀態由p、V和T刻劃，表達這幾個量之間的關係的方程稱之為氣體的狀態方程，不同的氣體有不同的狀態方程。但真實氣體的方程通常十分複雜，而理想氣體的狀態方程具有非常簡單的形式。
雖然完全理想的氣體並不可能存在，但許多實際氣體，特別是那些不容易液化、凝華的氣體（如氦、氫氣、氧氣、氮氣等，由於氦氣不但體積小、互相之間作用力小、也是所有氣體中最難液化的，因此它是所有氣體中最接近理想氣體的氣體。）在常溫常壓下的性質已經十分接近於理想氣體。
此外，有時只需要粗略估算一些數據，使用這個方程會使計算變得方便很多。
描寫理想氣體狀態變化規律的方程。對於一定質量的氣體，可以用壓強p和體積V來描述它的平衡態，而溫度T是p和V的函數，F(T,p,V)=0。這個關係式叫做氣體的狀態方程，它的具體形式需由實驗確定。玻意耳定律
又稱玻意耳—馬略特定律，是英國化學家R.玻意耳在1662年和法國物理學家E.馬略特在1679年分別獨立發現的。它的內容是：一定質量的氣體，當溫度保持不變時，壓強和體積成反比且乘積是一個常數：
p1V1=p2V2=p3V3=…或pV=C。
常數C 在不同溫度時有不同數值。
大量實驗結果表明，該定律對理想氣體完全正確。對於各種實際氣體，只要它的壓強不太高，溫度不太低，都近似地遵從此定律；氣體的壓強越低，它遵從玻意耳定律的精確度就越高。
一定質量的氣體，當體積不變時，它的壓強隨溫度作線性變化：
p=p0(1+αt),p
是0°C時的氣體壓強，p是t°C時的氣體壓強,α是在氣體體積不變時的壓強係數。對於理想氣體,α的數值為一普適常數，其值為1/273.15，於是：
若令T=t＋273.15，則上式簡化為：
pt=pαT,T
根據玻意耳定律、阿伏伽德羅定律和理想氣體溫標的定義，可以確定玻意耳定律中常數C與溫度的關係，並可導出：
式中p0、V0、T0為標準狀況下一摩爾理想氣體的壓強、體積、溫度；v為摩爾數。因此,的數值對各種氣都一樣。該數值叫摩爾氣體常數並用r表示：
於是式中M代表氣體的質量，μ 是氣體的分子量。這就是理想氣體狀態方程。
在壓強為幾個大氣壓以下時，各種實際氣體一般都近似地遵從理想氣體狀態方程。壓強越低，符合的程度越高。在壓強趨於零的極限情況下，一切氣體都嚴格地遵從它。根據理想氣體模型從氣體分子運動論出發，也可以推導出該物態方程。
摩爾氣體常數R R的數值可由一摩爾理想氣體在水的三相點 (273.16K)及一個大氣壓下的體積推出。也可以由一摩爾理想氣體在冰點 (273.15K)及一個大氣壓下的體積V0推出。用V0來推算的原因是V0可根據實驗結果求得比較準確的數值。由
V0=22.41383×10-3 m3 /mol
可算得
r=8.31441±0.00026J/(mol·K)。
計算氣體所含物質的量
從數學上說，當一個方程中只含有1個未知量時，就可以計算出這個未知量。因此，在壓強、體積、溫度和所含物質的量這4個量中，只要知道其中的3個量即可算出第四個量。這個方程根據需要計算的目標不同，可以轉換為下面4個等效的公式：
求壓強：
求體積：
求所含物質的量：
求溫度：
計算化學平衡問題
根據理想氣體狀態方程可以用於計算氣體反應的化學平衡問題。
根據理想氣體狀態方程可以得到如下推論：
溫度、體積恆定時，氣體壓強之比與所含物質的量的比相同，即可得Ρ平/P始=n平/n始
溫度、壓強恆定時，氣體體積比與氣體所含物質的量的比相同，即V平/V始=n平/n始
通過結合化學反應的方程，很容易得到化學反應達到平衡狀態后制定物質的轉化率。
實際氣體都不同程度地偏離理想氣體定律。偏離大小取決於壓力、溫度與氣體的性質，特別是取決於氣體液化的難易程度。對於處在室溫及1大氣壓左右的氣體，這種偏離是很小的，最多不過百分之幾。如氧氣和氫氣是沸點很低的氣體（-183攝氏度和-253攝氏度），在25攝氏度和1大氣壓時，摩爾體積與理想值的偏差在0.1%以內。而沸點較高的二氧化硫和氯氣(-10攝氏度與-35攝氏度)，在25攝氏度與1大氣壓下就不很理想。它們的摩爾體積比按理想氣體定律預計的數值分別低了24%與16%。當溫度較低、壓力較高時，各種氣體的行為都將不同程度地偏離理想氣體的行為。此時需要考慮分子間的引力和分子本身的體積重新構造氣體狀態方程。
根據理想氣體狀態方程可以用於計算氣體反應的化學平衡問題。
根據理想氣體狀態方程可以得到如圖示三推論。
通過結合化學反應的方程式，很容易得到化學反應達到平衡狀態后制定物質的轉化率。
p為理想氣體的壓強，單位通常為atm或kPa；
V為理想氣體的體積，單位為L或稱dm3；
n為理想氣體中氣體物質的量，單位為mol；
R為理想氣體常數、普適氣體恆量，更多值參見理想氣體常數； R=NK（N為阿伏伽德羅常數，Avgadro's number；K為玻爾茲曼常數，Boltzman number）
T為理想氣體的絕對溫度，單位為K
^ 在所有氣體當中，氦氣是構成粒子中最小的，氫氣僅次之。
^ 氦還是唯一不能在標準大氣壓下固化的物質。
^ 約合739mm
^ atm為標準大氣壓，
^ 當時查理認為是膨脹1/267，1847年法國化學家雷諾將其修正為1/273.15。
^ 其實查理早就發現壓力與溫度的關係，只是當時未發表，也未被人注意。直到蓋-呂薩克重新提出后，才受到重視。早年都稱“查理定律”，但為表彰蓋-呂薩克的貢獻而稱為“查理-蓋呂薩克定律”。
^ 如二氧化碳在40℃、52 MPa時，
基本信息
- 中文名
- 理想氣體狀態方程
- 外文名
- equation of state of ideal gas
- 別名
- 理想氣體定律
- 提出時間
- 1834
- 提出者
- 克拉伯龍
- 表達式
- pV=(mRT/M)=nRT