共找到2條詞條名為共軛曲線的結果 展開
- 機械中的共軛曲線
- 數學中的共軛曲線
共軛曲線
數學中的共軛曲線
如果在兩條曲線之間可以建立一個點對應,使得在對應點這兩條曲線有公共的主法線,則稱這兩條曲線為共軛曲線。
如果一條曲線有不與自身重合的共軛曲線,則稱其為Bertrand曲線。互為共軛的曲線 之間距離為常數,且在對應點間的切線成定角。
已知實現給定運動規律的瞬心線及共軛曲線中的一條曲線,求。這相當於由求的逆過程。
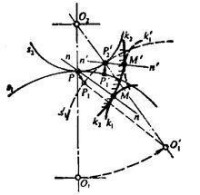
圖1
設給定瞬心線的中心距、傳動比 及共軛曲線中的一條曲線,求作嚙合線及。
如果在兩條曲線之間可以建立一個點對應,使得在對應點這兩條曲線有公共的主法線,則稱這兩條曲線為共軛曲線。

目錄