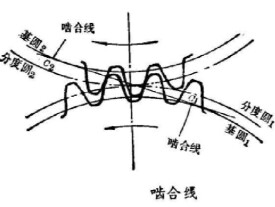
嚙合線
機械工程領域的數學曲線
齒輪在傳動過程中,各對輪齒的接觸點,總是落在兩基圓的內公切線上,由於各對輪齒的所有接觸點,在嚙合過程中總是沿著這條內公切線一點一點地依次前進,所以又稱它為嚙合線。
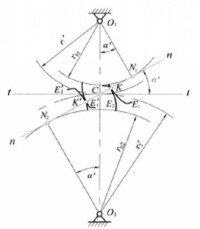
漸開線齒輪嚙合
右圖所示為一對漸開線齒廓在任意點K嚙合,過K點作兩齒廓的公法線,根據漸開線的性質,該公法線就是兩基圓的公切線,當兩齒廓轉到K'點嚙合時,過K'點所作公法線也是兩基圓的公切線。由於齒輪基圓的大小和位置均固定,漸開線齒廓公法線nn是唯一的,因此不管齒輪在哪點嚙合,嚙合點總是在這條齒廓公法線上,即嚙合線與齒廓公法線重合。由於齒輪傳動時正壓力沿著公法線方向傳遞,因此對於漸開線齒廓的齒輪傳動,嚙合線、過嚙合點的公法線、基圓的公切線和正壓力作用線四線合一。
嚙合線為一直線,漸開線齒廓的嚙合線必與公法線 相重合,所以嚙合線為一直線,嚙合線的直線性質使得傳遞壓力的方向保持不變,從而使傳動平穩。
漸開線圓柱齒輪副的嚙合線是一條與兩齒輪的基圓相切的內公切線,是一條直線。由於漸開線齒輪圓齒輪副每對共軛齒形均相同,故在傳動過程中這條直線的位置是不變的。也就是該直線與兩齒輪的中心連線的交點位置不變,因此可保證齒輪副有固定的傳動比。然而,非圓齒輪副則不同,原因是它的每對共軛齒形一般均不相同,故其齒形嚙合線也不相同。
非圓齒輪齒形嚙合線的求法如下:
(1)作圖法
由基本嚙合定理知:定平面中的兩齒形接觸點上的共法線通過復節曲線上的對應點。該對應點在復節曲線上的位置由非圓齒輪副的瞬時傳動比確定。因此,在求一對共軛齒形的嚙合線時,應該知道兩齒輪的中心距和其中一個齒輪的節曲線及齒形。
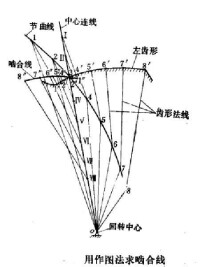
用作圖法求嚙合線
(2)解析法
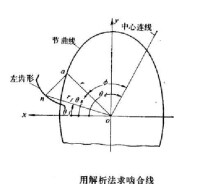
解析法求嚙合線
如右圖所示,設直角坐標系Oxy的原點O取在非圓齒輪的迴轉中心。兩齒 輪的中心連線與x軸的夾角 =常量。左齒形上某點n的齒形法線與節曲線交於a點。當齒輪轉過 角、a點落在中心連線上時,齒形上的n點與其共軛齒形上的對應點相切。這時的n點位置即齒形嚙合線上的點,其坐標值 和 可表示齒形嚙合線:
式中: ——齒形上n點的向徑;
——向徑與x軸的夾角。
右圖表示兩齒輪的一對齒正在嚙合,並設 為主動輪 的節圓;為從動輪 的節圓;NN為嚙合線。若 輪反時針方向轉動,則兩齒開始接觸時,必是 輪齒根部的一點和 輪齒頂上的a點相遇,這時的接觸點位置就在 輪齒頂和嚙合線的交點K;兩齒終止接觸,即將分開時,必是 輪齒頂部的b點和 輪齒根部的一點相遇,這時的接觸點位置就在 輪齒頂圓和嚙合線的交點。因此,圓中的一對齒嚙合時,接觸點在嚙合線上經過了KL的一段線,線段KL叫做嚙合線的長度。
將K和a點與中心 連接,又將b和L點與中心 連接,可得到中心角 和。
顯然,是輪 從兩齒在K點開始接觸到圖示位置為止所轉過的角度。這個角度 所決定的節圓弧長mn是從兩齒開始接觸到圖示位置為止,節圓 和 所滾過的弧長。
同樣,輪 須轉過 以使兩齒離開嚙合,即節圓須滾過一段弧長qp。所以在這一對齒嚙合的過程中,節圓 和 共滾過了弧,這一段節圓的弧長s叫做嚙合弧。嚙合弧的長度s也可以不用作圖方法,而按公式計算求得:
式中 是嚙合長度;是嚙合線傾斜角。
在右圖中,設齒輪的節圓是,節圓半徑是,NN是嚙合線,線段KL是 嚙合線長度,是基圓半徑,P是嚙合節點。當一對齒在嚙合過程中,接觸點經過KL長度,而齒輪 轉過 角。對應齒輪轉過的角,基圓應轉過一段弧長;而節圓轉過的弧長。
但是從圖上畫有陰影線的三角形可看出:
所以,把嚙合弧長度和齒輪周節相比較,如 就表示在一對齒離開嚙合(節圓滾過了弧s)時,后一對齒方才開始嚙合(節圓滾過了周節t表示后一對齒代替前一對齒)。同時嚙合的齒的對數越多,齒輪的轉動就越平滑,因此比率 可以代表齒輪轉動的平滑程度,我們把它叫做交接係數。交接係數不得小於1,否則前一對齒輪已經脫嚙合,后一對齒還沒有進入嚙合,齒輪就不可能連續的進行工作,這是絕對不允許的。交接係數應該取大於1的數,在粗傳動(低速傳動,不加工的齒輪)取。