轉軸傾角
轉軸傾角
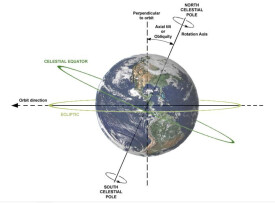
轉軸傾角,是指行星的自轉軸相對於軌道平面的傾斜角度,也稱為(obliguity)或軸交角(axial inclination)。在天文學,是以自轉軸與穿過行星的中心點並垂直於軌道平面的直線之間所夾的角度來表示與度量。
轉軸傾角也可以等效的表示為行星的軌道平面和垂直於自轉軸的平面所夾的角度。在太陽系,地球的軌道平面就是黃道,所以地球的轉軸傾角特別稱為黃赤交角,並以希臘字母的ε(Epsilon)作為表示的符號。
地球的轉軸傾角大約是23.44°(23°26’)。雖然在一整年之中轉軸傾角都朝著相同的方向,但是因為地球繞著太陽運行,因此原先朝向太陽的半球會逐漸改變成背離太陽的半球,反之亦然。這種作用是造成季節變化的主要原因,無論是那一個半球朝向太陽,那個半球每天的日照時間就會比較長,並且陽光在正午時間觸及地面的角度越接近垂直的方向,該地區在單位面積內得到的能量也越多。
低傾斜度造成極區接受到的太陽輻射減少,使得當地的環境有利於冰河作用。就像歲差和離心率的變化一樣,轉軸傾角的改變也會對季節變化造成重大的影響,只是在大冰河期開始時,轉軸傾角的周期對高緯度地區影響特別顯著。傾角的變化是一個造成冰河期或間冰期起伏的一個重要因素。
黃赤交角不是一個固定的值,會隨著時間而改變。這種變化是很緩慢的,稱為章動,精確的測量需要建立在每日數值變化的基礎上,而這是天文學家的工作。黃赤交角的變化和春分點的歲差是以相同的理論來計算,並且有相互的關連性。較小的ε意味著有較大的p(黃經歲差),反之亦然。實際上這兩種運動不僅是各自獨立的,並且在相互垂直的方向上。
從地球表面觀察和測量黃赤交角(ε)是天文學上很重要的知識和技能。觀察太陽在天球上隨著季節變化的位置,可以快速的掌握他的數值。測量在一年之中白天最長和最短的這兩天正午太陽的高度差,這個差值是黃赤交角的兩倍,在西元前1,000年的中國天文學家就是這樣確定黃赤交角的。
太陽一年當中在天球上最北和最南的赤緯就相等於轉軸傾角的角度。在一年當中,地球的轉軸朝向太陽的那一天也是白天最長的一天,太陽的赤經是+23°26’。一位在赤道上的觀測者,在全年的觀測中,當三月 (春分) 看見太陽在正午越過頭頂的正上方,然後會發現每天正午的太陽逐漸向北移動,直到6月(夏至)離開天頂的角度達到ε度,在9月(秋分)太陽又再回到頭頂的正上方,然後在12月(冬至)又距離天頂ε度。
又例如:在緯度50°的觀測者(無論南緯或北緯),在一年當中白天最長的那一天測得太陽在正午的高度是63° 26’,但在白天最短的那一天正午測得的高度只有16°34’,兩者的差是2ε=46°52’,所以ε=23°26’。
從算式可以得到距離地平的高度角:(90°-50°) + 23.4394° = 63.4394° (90° - 50°) - 23.4394° = 16.5606°
在赤道上,算式將被寫成 90° + 23.4394° = 113.4394° 和90° - 23.4394° = 66.5606° (永遠從正南方的地平線計算高度。).
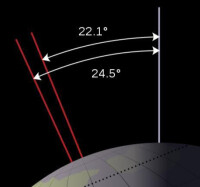
地球的偏角變化範圍在22.1° — 24.5°之間
太陽係數值模形
依據西蒙·紐康的計算,地球在19世紀末的轉軸傾角是23° 27’ 8.26” (1900年的曆元),而在望遠鏡能更精確的測量之前,這也是一般所接受的數值。電子計算機可以進行使更加精確的模型計算,在1976年,Lieske使用改良的模型得到黃赤交角的值ε = 23° 26’ 21.448” (2000年的曆元)。
這一部分在2000年已經成為國際天文聯合會推薦的簡要計算式中的一部分: ε = 84,381.448 − 46.84024 T − (59 × 10) T² + (1,813 × 10) T³,以秒為價算的單位, T是從星曆表2000.0曆元 (相當於儒略日 2,451,545.0) 起算的儒略世紀 (36,525日)。這個算式也適用紐康的計算數值,以線性的部分可以回推至1900年 (T = -1)。
觀察 T的線性部分是負值,所以現在的黃赤交角正在慢慢的減小。這個公式也暗示僅僅是在合理的 T範圍內給了ε一個近似值。如果不是這樣,當 T趨近於無限時,ε也會趨近無限。根據太陽係數值模形,顯示ε有著41,000年的循環周期,與分點歲差一樣有個常數值 (雖然不是歲差本身)。
其他的理論模型
其他的理論模型也許可以用更高階的 T展開來表演算ε的數值,但是因為沒有多項式 (有限的) 可以表現出周期性,當 T'增加至足夠大時,不是趨向正的無限大,就是負的無限大。因此您應該可以了解國際天文聯合會為何決定選擇與多數數學模型一致的一次方程式。在5,000年尺度內的過去和未來,可以滿足所有的模型,在9,000年尺度內的過去和未來,大部分仍有合理的準確性。而對更長遠的時代,彼此間的矛盾就太大了。
然而以外插法展開的平均多項式可以得到一條正弦曲線符合41,013年的周期,依據Wittmann,的公式,相當於:
ε = A + B sin ( C( T + D)),此處 A = 23.496932° ± 0.001200°, B = − 0.860° ± 0.005°, C = 0.01532 ± 0.0009 徑/儒略世紀, D = 4.40 ± 0.10儒略世紀,還有 T'是以2000.0曆元為起點的世紀數。
黃赤交角的平均範圍從22° 38’ 至 24° 21’,過去的最大值出現在西元前8,700年,均值是在1,500年,而未來的極小值將在11,800年。這個算式應該可以合理的推算過去以及未來數百萬年的概略數值。然而這個算式在振幅上表持著相同的數值,但是從米蘭科維奇循環的結果是有不規則的變化發生,其所引述的範圍是從21° 30’ 至 24° 30’,僅是低值就超越正常的22° 30’達1°之多。
如果我們往回追溯五百萬年,黃道面的傾角 (或許更精確地說應該是赤道在黃道上的移動) 會在22.0425° 至24.5044°,但是在未來的一百萬年,這個範圍只會在22.2289° 至24.3472°之間。
其他行星的轉軸傾角也會改變,例如火星的範圍相信是在15° 和 35°之間。地球的變動相對較小是歸因於月球穩定的影響,但並非永遠都是如此。依據沃德的說法,由於潮汐作用,在未來的15億年,地月的距離將從現在的60倍地球半徑增加至66.5倍地球半徑。這種情況一但發生,跟隨而來的行星共振效應將導致擺動的範圍在22° 至38°。在往後,大約20億年時,月球的距離達到68倍的地球半徑,其他的共振會造成更大幅度的震蕩,範圍從27°到60°,在氣候上將會有極端的變化。
| 天體 | 轉軸傾角 (°) |
| 水星 | ~0.01 |
| 金星 | 177.36 |
| 地球 | 23.439 281 |
| 月球 | 1.5424 |
| 火星 | 25.19 |
| 穀神星 (矮行星) | ~4 |
| 智神星 | ~60 |
| 木星 | 3.13 |
| 土星 | 26.73 |
| 天王星 | 97.77 |
| 海王星 | 28.32 |
| 冥王星 | 119.61 |
| 鬩神星 (矮行星) | 不詳 |