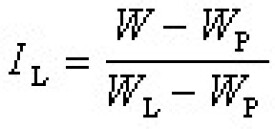隨機文法
隨機文法
隨機文法,是計算機語言中隨機文法對每條文法產生式(重寫規則)賦予一定的概率值以描述隨機模式的文法。這種高維隨機文法和語言能夠有效地描述帶有雜訊與畸變的比較複雜的模式。
目錄
對每條文法產生式(重寫規則)賦予一定的概率值以描述隨機模式的文法。由隨機文法產生的語言稱為隨機語言,接受隨機語言的自動機稱為隨機自動機。在通信、信息存儲和檢索以及物理模式的測量處理等問題中不可避免地存在雜訊和干擾,因此用於描述模式類的語言帶有隨機性質。為了從數學上表徵語言 L的不確定性和隨機性,可以在文法產生式中引入概率度量pij,即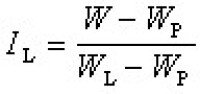 ,且
,且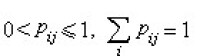 。
。
隨機文法
隨機文法
設從起始符s開始通過使用產生式序列r1,r2,…,rm導出鏈x,與產生式r1,…,rm 相聯繫的概率分別是p(r1),p(r2),…,p(rm),當概率 p(ri)(i=1,…,m)的大小不依賴於在它前面導出過程所使用的產生式時,則用上述序列導出句子x的概率是
隨機文法
按照短語結構文法中αi→βj的不同限制條件,相應的有 0型(無限制)、1型(上下文敏感)、2型(上下文無關)和3型(有限狀態)四種類型隨機文法。
隨機文法中的一個重要理論問題就是確定一致性條件,即文法所產生的全部句子的導出概率的和應等於1的條件。對於產生式形式為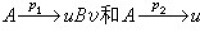 (A,B為非終止符,u,v為終止符)的線性文法和上下文無關隨機文法的一致性條件的檢驗,可分別利用有限狀態馬爾可夫過程和蓋爾頓-華生分支理論來確定。隨機上下文敏感文法的一致性問題,至今尚未得到解決。
(A,B為非終止符,u,v為終止符)的線性文法和上下文無關隨機文法的一致性條件的檢驗,可分別利用有限狀態馬爾可夫過程和蓋爾頓-華生分支理論來確定。隨機上下文敏感文法的一致性問題,至今尚未得到解決。
隨機文法
當把隨機的概念應用到高維隨機文法時,就得到隨機樹文法和相應的隨機樹語言、隨機圖文法和相應的隨機圖語言等。這種高維隨機文法和語言能夠有效地描述帶有雜訊與畸變的比較複雜的模式。