貝爾函數
貝爾函數
在研究函數的連續性基礎上產生的一類重要的函數。R.L.貝爾於1899年提出如下的函數分類方法:以區間【0,1】上的函數為例,【0,1】上的連續函數稱為0類函數。0類函數序列點點收斂的極限函數,當它不是0類函數時,就稱為1類函數。1類函數序列點點收斂的極限函數,如果不是0類或1類的函數時,便稱為2類函數。依次對每一個自然數n,可以引入n類函數的概念。
在研究函數的連續性基礎上產生的一類重要的函數。R.L.貝爾於1899年提出如下的函數分類方法:以區間【0,1】上的函數為例,【0,1】上的連續函數稱為0類函數。0類函數序列點點收斂的極限函數,當它不是0類函數時,就稱為1類函數。1類函數序列點點收斂的極限函數,如果不是0類或1類的函數時,便稱為2類函數。依次對每一個自然數n,可以引入n類函數的概念。如果{ƒυ},v=1,2,…,ƒυ是nυ類函數,{nυ}是自然數列的子序列,{ƒυ}點點收斂於ƒ(x),當ƒ(x)不是任何n類函數(n是自然數),稱ƒ(x)是ω類函數。如此再繼續定義ω+1,ω+2,…類函數。用超限歸納法對一切序數η,都可以定義η類函數。所有這些類的函數統稱為貝爾函數,而貝爾函數的全體稱為貝爾函數類。【0,1】上的狄利克雷函數D(x)(它在有理點上取值為1,無理點上取值為零)不是1類函數,但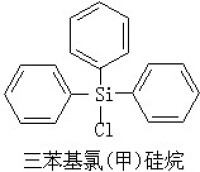 ,所以D(x)是2類函數。可以證明,當序數α<α1(α1是第一個不可列的序數)時,α類是不空的,但α1類是空集。另外,貝爾函數類的勢(或基數)與【0,1】的勢相等。但【0,1】上所有實函數的勢大於【0,1】的勢。因此定義在【0,1】上的函數中有很多不是貝爾函數。貝爾函數類的另一等價的定義是:包含連續函數全體且對點點收斂的極限運算封閉的最小函數類。
,所以D(x)是2類函數。可以證明,當序數α<α1(α1是第一個不可列的序數)時,α類是不空的,但α1類是空集。另外,貝爾函數類的勢(或基數)與【0,1】的勢相等。但【0,1】上所有實函數的勢大於【0,1】的勢。因此定義在【0,1】上的函數中有很多不是貝爾函數。貝爾函數類的另一等價的定義是:包含連續函數全體且對點點收斂的極限運算封閉的最小函數類。

貝爾函數
類似地,在n維空間與一般的拓撲空間也可引入貝爾函數類。
波萊爾集深入討論函數的連續性、可微性、可積性時必不可少的重要集類。設G、F分別表示 n維歐幾里得空間Rn中開集、閉集全體。凡是能表示成G(或F)中一列集{An}的交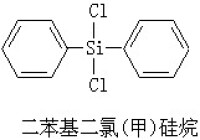 (或和
(或和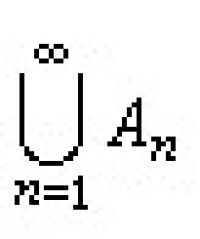 )的集的全體記為Gδ(或Fσ)。凡能表示成Gδ(或Fσ)中一列集{An} 的和
)的集的全體記為Gδ(或Fσ)。凡能表示成Gδ(或Fσ)中一列集{An} 的和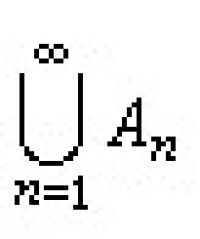 (或交
(或交 )的集的全體記為Gδσ(或Fσδ),如此又繼續可以定義出新的集類Gδσδ、Fσδσ,…。同貝爾函數類一樣,對一切序數可用超限歸納法來依次定義新的集類。同樣可以證明:當序數α<α1時,上述定義能產生新類型的集,而從α1開始就不再產生新類型集了。由上述方式得到的每個集稱為Rn上的波萊爾集。波萊爾集全體稱為 Rn上波萊爾集類(也稱波萊爾域),記為B(Rn)。波萊爾集類還有幾種等價的定義:B(Rn)是包含Rn中一切有限“立方體”的最小σ環;B(Rn)是包含Rn中一切開集的最小σ環;B( Rn)是包含Rn中一切閉集的最小σ環。(見測度論)
)的集的全體記為Gδσ(或Fσδ),如此又繼續可以定義出新的集類Gδσδ、Fσδσ,…。同貝爾函數類一樣,對一切序數可用超限歸納法來依次定義新的集類。同樣可以證明:當序數α<α1時,上述定義能產生新類型的集,而從α1開始就不再產生新類型集了。由上述方式得到的每個集稱為Rn上的波萊爾集。波萊爾集全體稱為 Rn上波萊爾集類(也稱波萊爾域),記為B(Rn)。波萊爾集類還有幾種等價的定義:B(Rn)是包含Rn中一切有限“立方體”的最小σ環;B(Rn)是包含Rn中一切開集的最小σ環;B( Rn)是包含Rn中一切閉集的最小σ環。(見測度論)

貝爾函數
貝爾函數
貝爾函數

貝爾函數
在一般拓撲空間中可類似地引入波萊爾集類。
貝爾函數與波萊爾可測函數 設ƒ是拓撲空間Χ上的實函數,如果對任何實數с,集{x│ƒ(x)<с}是波萊爾集,則稱ƒ是Χ上的波萊爾可測函數。Χ上的貝爾函數都是Χ上的波萊爾可測函數。同樣,設E是Χ的子集,如果E的特徵函數IE(即在E上值為1,E的余集上值為0的函數)是Χ上的貝爾函數,則稱E是貝爾集。貝爾集都是波萊爾集。當Χ=Rn時,波萊爾可測函數(波萊爾可測集)都是貝爾函數(貝爾集)。
解析集 深入研究直線上波萊爾集與勒貝格可測集的關係時發現的重要集類,它們在近代隨機過程中有廣泛的應用。設(Ω,F)是可測空間,E為緊的度量空間,記K(E)×F={A×F是E中的緊集,F∈F},(K(E)×F)σδ是K(E)×F中的集作可列和后再進行可列交的運算而得到的集類。設B∈(K(E)×F)σδ,稱B在Ω上的投影Ⅱ(B)為Ω中的F解析集。它們的全體記為φ(F)。若用P表示(Ω,F)上的概率測度全體,Fp(p∈P)表示F用p作完全化擴張而得到的σ代數,則利用喬格的容度理論可證明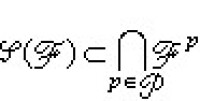 。
。
貝爾函數
特別,當E=Rn,n=1,2…,Ω=【0,1】,F=B【0,1】時,EX【0,1】上的波萊爾集在【0,1】上的投影是解析集,並且φ(F)是【0,1】上勒貝格可測集類的真子集。