馬赫錐

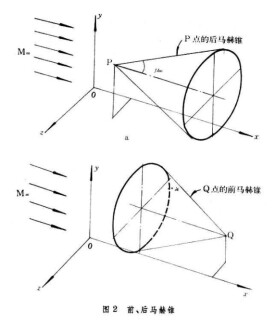
當一個微弱的點擾源(如尖頭彈丸的頂尖)以超聲速在大氣中運動或位於超聲速勻直流中時，存在一個以點擾源為頂點、把空間分為擾動區和未擾動區的錐面，稱為馬赫錐，錐的半頂角稱為馬赫角。它是奧地利物理學家E.馬赫於1887年在分析彈丸擾動的傳播圖形時首先提出的，因而得名。

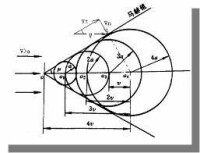
微弱擾動使氣體的速度、壓強、密度和溫度等發生微小的變化，並以聲速相對於氣體而傳播。馬赫錐的形成可用點擾源的運動來說明。若點擾源以超聲速在空氣中作等速直線運動，則一秒鐘后，擾源由點（經點）到達點，走過的距離等於。這時，在點產生的擾動擴展到以點為中心、速度為半徑的球面上。由於故點在以為中心的圓外。擾源於等點產生的擾動，也分別擴展到相應的球面上。馬赫錐就是以直線為母線的錐面，這個錐面就是那些球面的包絡面。錐面的半頂角為馬赫角()。隨著擾源向前運動，馬赫錐也作為一個波面往前傳播，故有時也稱馬赫波。若取隨擾源運動的相對坐標系，則成為定常超聲速流中的馬赫錐。對於二維平面流動，馬赫錐退化為兩條直線，稱為馬赫線。若擾源以亞聲速運動，則產生的擾動可傳到擾源之前，因而不形成馬赫錐。