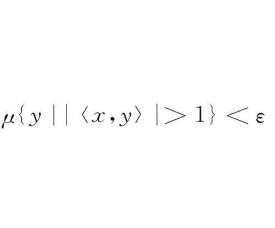柱測度
柱測度
柱測度(cylinder measure)是測度概念的推廣。設X,Y是兩個實線性空間,〈x,y〉(x∈X,y∈Y)是X×Y上的實雙線性泛函,且對任意非零向量x∈X,存在y∈Y,使得〈x,y〉≠0,對Y也有同樣的假定,任取n個向量xi∈X(1≤i≤n),記Y中使〈x1,·〉,〈x2,·〉,…,〈xn,·〉均為可測函數的最小σ代數為F(x1,x2,…,xn),每個F(x1,x2,…,xn)中的集稱為Y中的柱集,柱集全體記為F,它是Y上的代數。若μ是F上的集函數且μ限制在每一個F(x1,x2,…,xn)上是一個概率測度,則μ稱為Y上的柱測度。明洛斯(Р.А.Минлос)於1959年證明了下面的基本定理:若Φ是核空間,則Φ的共軛空間Φ′的任何一個關於Φ的拓撲連續的(即對任何ε>0,存在Φ中點o的鄰域U,對任何x∈U,都有μy||﹤x,y﹥|>1<ε。柱測度μ都是可列可加的。
柱測度
柱測度
柱測度
柱測度
設 是線性空間,是 上某些線性泛函所成的線性空間,設S是 中的Borel柱全體所成的代數。
柱測度
柱測度
柱測度
柱測度
設P是S上的集函數;對於 的每個有限維子空間,把P限制在相應於中的Borel柱全體 上時,P是概率測度,那麼稱P是 上的 柱測度。
顯然,柱測度P又滿足下面的條件:
柱測度
柱測度
(iii) P是有限可加的。
柱測度
柱測度
柱測度
當柱測度P在S上可列可加的時候,我們根據熟知的方法,把P延拓到包含S的最小 代數 上——延拓后的集函數仍記做P,——使得 成為 概率測度空間。
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
設P 是 上的柱測度,若 是 上的函數,而且存在 的有限維子空間 使 關於概率測度空間 是可積的,那麼稱 關於 上的柱測度P是可積的,而且以 關於 的積分作為 關於柱測度P的積分,仍記為
柱測度
柱測度
柱測度
特別,當P是可列可加的時候,這個積分值也就是 關於測度空間的積分。
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
引理1 設 是線性空間,是 上某些線性泛函組成的線性空間,P是 上的柱測度,作函數
柱測度
柱測度
柱測度
則f是 上的正定準連續函數,而且。
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
引理2 設 是線性空間,是 上某些線性泛函組成的線性空間,又是完整的(即 中的非零泛函的零空間只含零向量),那麼對於 上的每個正定準連續函數 必有 上唯一的柱測度P,使得
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
定義2設 是以 做拓撲的線性拓撲空間,是 上的某些線性泛函組成的線性空間,P 是 上的柱測度,如果對於任何正數 必有0的環境,使得當 時,
柱測度
柱測度
成立,那麼稱P是關於拓撲 連續的或簡稱P是連續的。
柱測度
柱測度
柱測度
柱測度
引理3 設 是線性拓撲空間,是 上的某些線性泛函組成的線性空 間,P 是上的柱測度,作
柱測度
柱測度
那麼f 在 上連續的充要條件是柱測度P為連續的。
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
柱測度
定理1設 是滿足第一可列公理的線性拓撲空間,是 上某些線性連續泛函所成的線性空間 是 中包含一切Borel柱的最小 代數,是概率測度空間,則P必是連續的。