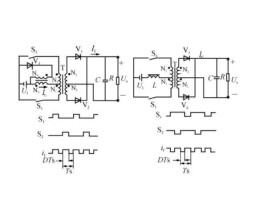
電路變換

電路變換的連接方式多半比較簡單，即使不簡單，也能為計算提供一定的方便。最常見到的電路變換是等效變換。這是一種能保證電路的非變換部分中的電壓、電流在變換中維持不變的變換。

已經證明，要保證非變換部分中的電壓、電流維持不變，變換成的新電路部分必須是變換部分的等效電路，亦即前者與後者應具有相同的外特性。所以，實現這種變換的關鍵是求出電路變換部分的等效電路。求等效電路的步驟是：首先，根據電路變換部分的電路圖用適當的方法寫出該部分的外特性方程；然後，根據求得的外特性方程確定等效電路的連接方式（拓撲結構）和相應的元件參數。

把電路內一個由電阻元件連接成的多射線星形變換成一個多角形是這類變換中的一個較為典型的實例。按上述步驟完成這個變換應首先寫出多射線星形的外特性方程。

在電路計算中，把幾個串聯（或並聯）的同類元件合併成一個元件是最簡單的等效變換。戴維南定理和諾頓定理中的等效替換，以及電源模型間的互換也都是等效變換。雖然替代定理中所進行的替代是根據外特性曲線上的一點相同，而不是整個曲線相同，但因一點相同仍含有等效的意思，故可看成是一種特殊的等效變換。

含受控源電路變換控制量解法初探

隨著有源元件的廣泛使用，含受控源電路的分析也顯得越來越重要。在含受控源的電路中，各支路的響應除了受到網路拓樸約束外，又增加了新的約束，因而使得分析計算增加了難度。在用等效變換的方法化簡含受控源的電路時，一般認為，受控源可以當作獨立源一樣參與變換，而控制量則不能變換掉。這就使得等效變換的思路受到了限制，影響了電路的化簡。然而，分析表明，控制量是可以進行變換的。

眾所周知，一個電路中各部分的電流、電壓都要受到基爾霍夫定律、歐姆定律的約束，作為控制量的電流或電壓自然也不例外。這就意味著，作為控制量的某個電流或電壓可以用其它的電流、電壓來表示。換句話說，我們可以找一個量作為新的控制量，利用基爾霍夫定律、歐姆定律進行控制量的“轉移”即變換，從而使原控制量所在支路也能與其它支路一樣參與電路的等效變換。

在對電路進行等效化簡時，原控制量與其所在支路消失了，但該支路的兩個端紐卻可以保留下來，因為它們實際上也是原始電路的兩個節點，故它們也同時屬於該支路相連接的外電路。而在變換后的電路中，這兩個端紐之間的電壓又可以用新的形式來表示，並參與電路的計算。在變換控制量的同時，受控源仍然可以當作獨立電源來處理，即將受控電壓源、電阻串聯組合與受控電流源、電導的並聯組合相互進行等效變換。這樣，就有可能將含受控源的電路最終化簡成單迴路電路從而使計算過程變得簡便。

由以上分析可知：用等效變換方法分析含受控源的電路時，控制量也是可以變換的，從而使原控制量所在支路與其它支路一樣參與電路變換，也使等效變換這一方法更充分地發揮其化簡電路的作用，使等效電路更為簡單，運算更為簡便；以原控制量所在支路的支路電壓作為新控制量，簡單、方便、容易掌握和運用。

負反饋放大電路變換分析法的討論

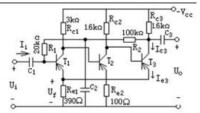
對負反饋放大電路，可以認為信號只通過基本放大電路，從輸入端傳 送到輸出端，反饋信號只通過反饋網路反饋到輸入端，反饋係數與信號源內阻及負載無關。因此可以按照一定的變換規律得到即斷開反饋又考慮了反饋網路負載效應的放大電路。由於可以直接從這個電路中求出反饋係數，故將其稱為基本反饋電路。然後求出基本反饋電路的開環增益和反饋係數，再根據負反饋的一般公式，計算有反饋時的閉環增益、輸入電阻和輸出電阻，這種負反饋放大電路的分析方法既稱為變換分析法。用變換分析法分析負反饋放大電路時，關鍵在於要按照一定的變換規律把負反饋放大電路變換為基本反饋電路，而反饋網路應包含在基本反饋電路中，但僅起到負載的作用。

負反饋放大電路變換為反饋電路的一般規律

（1）如何從負反饋放大電路中找出基本反饋電路輸出迴路

從負反饋放大電路輸入端看：如果是串聯反饋 ,將負反饋放大電路輸入端開路；如果是並聯反饋，將負反饋放大電路輸入端短路()；從負反饋放大電路輸出端得到的交流通路即為基本反饋電路輸出迴路的交流通路。

（2）如何從負反饋放大電路中找出基本反饋電路輸入迴路

從負反饋放大電路輸出端看：如果是電壓反饋，將負反饋放大電路輸出端短路()；如果是並聯反饋，將負反饋放大電路輸出端開路()；從負反饋放大電路輸入端得到的交流通路即為基本反饋電路輸入迴路的交流通路。經過以上變換，可求得即斷開反饋又考慮了反饋網路負載效應的基本反饋電路。

負反饋放大電路動態參數的計算步驟

(1) 確定反饋類型，依照變換分析法，從負反饋放大電路中求出基本反饋電路；

(2) 在基本反饋電路中求出反饋係數F，開環增益A；

(3) 求出反饋深度；

(4) 利用反饋深度，結合負反饋放大電路，求出閉環增益、輸入電阻、輸出電阻。

從以上分析舉例可看出，對多級反饋放大電路，利用這種方法可歸結為計算基本反饋電路的反饋係數和開環增益，然後利用負反饋的一般公式，結合負反饋放大電路，計算出有反饋時的閉環增益、輸入電阻和輸出電阻，優點是物理概念清楚，比較直觀。