歐姆定律
某段導體的電流跟電壓成正比,跟電阻成反比
歐姆定律的簡述是:在同一電路中,通過某段導體的電流跟這段導體兩端的電壓成正比,跟這段導體的電阻成反比。該定律是由德國物理學家喬治·西蒙·歐姆1826年4月發表的《金屬導電定律的測定》論文提出的。
隨研究電路工作的進展,人們逐漸認識到歐姆定律的重要性,歐姆本人的聲譽也大大提高。為了紀念歐姆對電磁學的貢獻,物理學界將電阻的單位命名為歐姆,以符號Ω表示。
常見簡述:在同一電路中,通過某一導體的電流跟這段導體兩端的電壓成正比,跟這段導體的電阻成反比,這就是歐姆定律。
標準式:
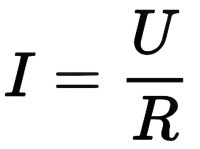
歐姆定律
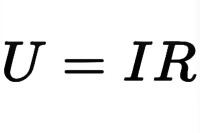
歐姆定律
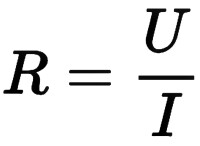
歐姆定律
(變形公式: ; )
注意:公式中物理量的單位:I:(電流)的單位是安培(A)、U:(電壓)的單位是伏特(V)、R :(電阻)的單位是歐姆(Ω)。
部分電路公式:I=U/R,或I=U/R=P/U(I=U:R)
(由歐姆定律的推導式【U=IR;R=U/I】不能得到①:電壓即為電流與電阻之積;②:電阻即為電壓與電流的比值。所以,這些變形公式僅作計算參考,並無具體實際意義。)
歐姆定律成立時,以導體兩端電壓為橫坐標,導體中的電流I為縱坐標,所做出的曲線,稱為伏安特性曲線。這是一條通過坐標原點的直線,它的斜率為電阻的倒數。具有這種性質的電器元件叫線性元件,其電阻叫線性電阻或歐姆電阻。
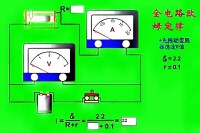
全電路公式:I=E/(R+r)
E為電源電動勢,單位為伏特(V);R是負載電阻,r是電源內阻,
單位均為歐姆符號是Ω.I的單位是安培(A).

歐姆定律
詹姆斯·麥克斯韋詮釋歐姆定律為,處於某狀態的導電體,其電動勢與產生的電流成正比。因此,電動勢與電流的比例,即電阻,不會隨著電流而改變。在這裡,電動勢就是導電體兩端的電壓。參考這句引述的上下文,修飾語“處於某狀態”,詮釋為處於常溫狀態,這是因為物質的電阻率通常相依於溫度。根據焦耳定律,導電體的焦耳加熱(Joule heating)與電流有關,當傳導電流於導電體時,導電體的溫度會改變。電阻對於溫度的相依性,使得在典型實驗里,電阻相依於電流,從而很不容易直接核對這形式的歐姆定律。
在以前的實驗中,歐姆使用的電池組是伏打電堆,這種電堆的電動勢不穩定,使他大為頭痛。後來經人建議,改用鉍銅溫差電偶作電源,從而保證了電源電動勢的穩定。
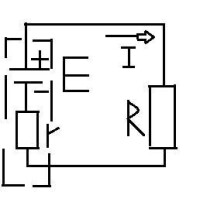
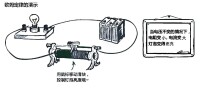
1826年,歐姆用上面圖中的實驗裝置導出了他的定律。在木質座架上裝有電流扭力秤,DD'是扭力秤的玻璃罩,CC'是刻度盤,s是觀察用的放大鏡,m和m'為水銀杯,abb'a'為鉍框架,鉍、銅框架的一條腿相互接觸,這樣就組成了溫差電偶。A、B是兩個用來產生溫差的錫容器。實驗時把待研究的導體插在m和m'兩個盛水銀的杯子中,m和m'成了溫差電池的兩個極。
歐姆準備了截面相同但長度不同的導體,依次將各個導體接入電路進行實驗,觀測扭力拖拉磁針偏轉角的大小,然後改變條件反覆操作,根據實驗數據歸納成下關係:
x=q/(b+l)式中x表示流過導線的電流的大小,它與電流強度成正比,A和B為電路的兩個參數,L表示實驗導線的長度。
1826年4月歐姆發表論文,把歐姆定律改寫為:X=KSA/L,s為導線的橫截面積,K表示電導率,A為導線兩端的電勢差,L為導線的長度,X表示通過L的電流強度。如果用電阻l'=L/KS代入上式,就得到X=A/I'這就是歐姆定律的定量表達式,即電路中的電流強度和電勢差成正比而與電阻成反比。為了紀念歐姆對電磁學的貢獻,物理學界將電阻的單位命名為歐姆,以符號Ω表示。1歐姆定義為電位差為1伏特時恰好通過1安培電流的電阻。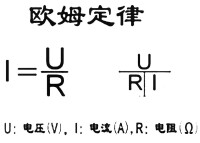

歐姆定律
1825年5月歐姆在他的第一篇科學論文中發表電流產生的電磁力的衰減與導線長度的關係,是有關伽伐尼電路的論文,但其中的公式是錯誤的。
1826年4月歐姆改正了這個錯誤,得出有名的歐姆定律。
1827年出版了他最著名的著作《伽伐尼電路的數學論述》,文中列出了公式,明確指出伽伐尼電路中電流的大小與總電壓成正比,與電路的總電阻成反比,式中S為導體中的電流強度(I),A為導體兩端的電壓(U),L為導體的電阻(R),可見,這就是今天的部分電路歐姆定律公式。
1876年,詹姆斯·麥克斯韋與同事,共同設計出幾種測試歐姆定律的實驗方法,能夠特別凸顯出導電體對於加熱效應的響應。
歐姆定律
歐姆定律
導率(傳導率)進行研究。
1826年4月歐姆發表論文,把歐姆定律改寫為:x=ksa/ls為導線的橫截面積,K表示電導率,A為導線兩端的電勢差,L為導線的長度,X表示通過L的電流強度。如果用電阻l'=l/ks代入上式,就得到X=a/I'這就是歐姆定律的定量表達式,即電路中的電流強度和電勢差成正比而與電阻成反比。
歐姆定律只適用於純電阻電路,金屬導電和電解液導電,在氣體導電和半導體元件等中歐姆定律將不適用。
設有一段金屬導體,橫截面積為S,長為L,在導體的兩端加上電壓U,則導體中的場強E=U/L.這時,一自由電子在電場力F=eE的作用下做定向移動。設電子的質量為m,則定向移動的加速度為a=F/m=eE/m=U(e/mL)。
運動的自由電子要頻繁地與金屬正離子碰撞,使其定向移動受到破壞,限制了移動速率的增加。自由電子在碰撞後向各個方向彈射的機會相等,失去了之前定向移動的特性,又要從新開始做初速為0的定向加速運動。
自由電子相繼兩次碰撞的間隔有長有短,設平均時間為t,則自由電子在下次碰撞前的定向移動速率vt(以t為下標)=at,那麼在時間t內的平均速率v=at/2。結合之前推出的a=U(e/mL),得自由電子的平均移動速率為v=U(et/2mL)。
代入電流的微觀表達式I=neSv,得I=U(neSt/2mL)
對於一定的金屬材料,在一定的溫度下,t是個確定的數值(10~10s),也就是說,對於一段金屬導體,neSt/2mL是個常量。
因此,導體中的電流強度I與兩端的電壓U成正比。導體兩端的電壓與導體中的電流強度的比值(2mL/neSt)就是這段導體的電阻。由此看出,導體的電阻與長度成正比,與橫截面積成反比,與1/ne^2t成正比。1/net由導體的特性決定。因此,在一定溫度時,導體的電阻是R=ρL/S。ρ是導體的電阻率。對於一定溫度與相同的導體,電阻率一定。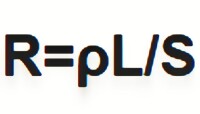
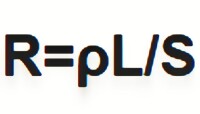
歐姆定律
在通常溫度或溫度不太低的情況下,對於電子導電的導體(如金屬),歐姆定律是一個很準確的定律。當溫度低到某一溫度時,金屬導體可能從正常態進入超導態。處於超導態的導體電阻消失了,不加電壓也可以有電流。對於這種情況,歐姆定律當然不再適用了。
在通常溫度或溫度變化範圍不太大時,像電解液(酸、鹼、鹽的水溶液)這樣離子導電的導體,歐姆定律也適用。而對於氣體電離條件下,所呈現的導電狀態,和一些導電器件,如電子管、晶體管等,歐姆定律不成立。
電機工程學和電子工程學
在電機工程學和電子工程學里,歐姆定律妙用無窮,因為它能夠在宏觀層次表達電壓與電流之間的關係,即電路元件兩端的電壓與通過的電流之間的關係。
物理學
在物理學里,對於物質的微觀層次電性質研究,會使用到的歐姆定律,以矢量方程表達,處於均勻外電場的均勻截面導電體(例如,電線)。
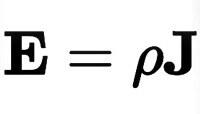
歐姆定律1
在導體內任意兩點g、h,定義電壓為將單位電荷從點g移動到點h,電場力所需做的機械功:
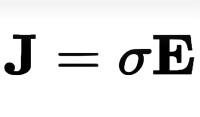
歐姆定律
其中,Vgh是電壓,w是機械功,q是電荷量,dL 是微小線元素。
假設,沿著積分路徑,電流密度J=jI為均勻電流密度,並且平行於微小線元素:
dL=dlI;其中,I是積分路徑的單位矢量。
那麼,可以得到電壓:
Vgh=Jρl;其中,l是積分路徑的徑長。
假設導體具有均勻的電阻率,則通過導體的電流密度也是均勻的:
J=I/a;(黑體字部分為矢量(台灣稱做向量)其中,a是導體的截面面積。
電壓Vgh簡寫為V。電壓與電流成正比:
V=Vgh=Iρl/a。總結,電阻與電阻率的關係為
R= ρl/a。假設J> 0 ,則V> 0 ;將單位電荷從點g移動到點h,電場力需要作的機械功w> 0 。所以,點g的電勢比點h的電勢高,從點g到點h的電勢差為V。從點g到點h,電壓降是V;從點h到點g,電壓升是V。
給予一個具有完美晶格的晶體,移動於這晶體的電子,其運動等價於移動於自由空間的具有有效質量(effective mass)的電子的運動。所以,假設熱運動足夠微小,周期性結構沒有偏差,則這晶體的電阻等於零。但是,真實晶體並不完美,時常會出現晶體缺陷(crystallographic defect),有些晶格點的原子可能不存在,可能會被雜質侵佔。這樣,晶格的周期性會被擾動,因而電子會發生散射。另外,假設溫度大於絕對溫度,則處於晶格點的原子會發生熱震動,會有熱震動的粒子,即聲子,移動於晶體。溫度越高,聲子越多。聲子會與電子發生碰撞,這過程稱為晶格散射(lattice scattering)。主要由於上述兩種散射,自由電子的流動會被阻礙,晶體因此具有有限電阻。
凝聚態物理學研究物質的性質,特別是其電子結構。在凝聚態物理學里,歐姆定律更複雜、更廣義的方程非常重要,屬於本構方程(constitutive equation)與運輸係數理論(theory of transport coefficients)的範圍。
歐姆定律及其公式的發現,給電學的計算,帶來了很大的方便。這在電學史上是具有里程碑意義的貢獻。 1854年歐姆與世長辭。十年之後英國科學促進會為了紀念他,將電阻的單位定為歐姆,簡稱“歐”,符號為Ω,它是電阻值的計量單位,在國際單位制中是由電流所推導出的一種單位。