小波去噪
小波去噪
目錄
wavelet domain denoising
近年來,小波理論得到了非常迅速的發展,而且由於其具備良好的時頻特性,因而實際應用也非常廣泛。在去噪領域中,小波理論也同樣受到了許多學者的重視,他們應用小波進行去噪並獲得了非常好的效果。具體來說小波去噪方法的成功主要得益於小波變換具有如下特點:
(1)低熵性,小波係數的稀疏分佈,使得圖象變換后的熵降低;
(2)多解析度,由於採用了多解析度的方法,所以可以非常好地刻畫信號的非平穩特徵,如邊緣、尖峰、斷點等;
(4)選基靈活性,由於小波變換可以靈活選擇變換基,從而對不同應用場合,對不同的研究對象,可以選用不同的小波母函數,以獲得最佳的效果。
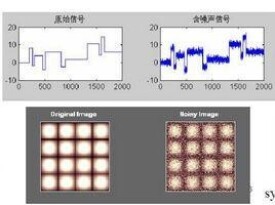
小波去噪方法包括三個基本的步驟:對含雜訊信號進行小波變換;對變換得到的小波係數進行某種處理,以去除其中包含的雜訊;對處理后的小波係數進行小波逆變換,得到去噪后的信號。小波去噪方法的不同之處集中在第一步。
小波去噪問題的描述
在數學上,小波去噪問題的本質是一個函數逼近問題,即如何在由小波母函數伸縮和平移版本所展成的函數空間中,根據提出的衡量準則,尋找對原信號的最佳逼近,以完成原信號和雜訊信號的區分。也就是尋找從實際信號空間到小波函數空間的最佳映射,以便得到原信號的最佳恢復。
從信號學的角度看,小波去噪是一個信號濾波的問題,而且儘管在很大程度上小波去噪可以看成是低通濾波,但是由於在去噪后還能成功地保留信號特徵,所以在這一點上又優於傳統的低通濾波器。由此可見,小波去噪實際上是特徵提取和低通濾波功能的綜合,其流程框圖如圖所示。
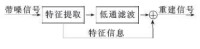
小波去噪框圖
實質是減少剔除雜訊產生的小波係數,最大限度的保留真實信號的係數。
小波反變換得到信號的最優估計。
基本方法:
模極大值重構去噪
空域相關去噪
小波閾值去噪