垂徑定理
數學幾何(圓）中的定理
垂徑定理是數學幾何(圓）中的一個定理，它的通俗的表達是：垂直於弦的直徑平分弦且平分這條弦所對的兩條弧。數學表達為：如圖，直徑DC垂直於弦AB，則AE=EB，弧AD等於弧BD（包括優弧與劣弧），半圓CAD=半圓CBD。
垂直於弦的直徑平分這條弦，並且平分弦所對的兩條弧。
一條直線，在下列5條中只要具備其中任意兩條作為條件，就可以推出其他三條結論。稱為知二得三（知二推三）。
平分弦所對的優弧
平分弦所對的劣弧（前兩條合起來就是：平分弦所對的兩條弧）
平分弦（不是直徑）
垂直於弦
過圓心
1.
平分弦所對的優弧
2.
平分弦所對的劣弧（前兩條合起來就是：平分弦所對的兩條弧）
3.
平分弦（不是直徑）
4.
垂直於弦
5.
過圓心
| 如圖，在⊙O中，DC為直徑， AB是弦，AB⊥DC於點E，AB、CD交於E，求證：AE=BE，弧AC=弧BC，弧AD= 弧BD | |
|---|---|
| 證明 | 圖示 |
連接OA、OB分別交⊙O於點A、點B ∵OA、OB是⊙O的半徑 ∴OA=OB ∴△OAB是等腰三角形 ∵AB⊥DC ∴AE=BE，∠AOE=∠BOE（等腰三角形三線合一） ∴弧AD=弧BD，∠AOC=∠BOC ∴弧AC=弧BC | 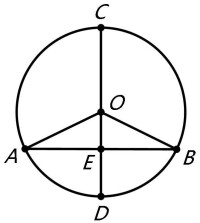 垂徑定理圖示 |
原本命題，其中CD垂直於直線AB
幾何語言：∵DC是直徑，AE=EB
∴直徑DC垂直於弦AB，劣弧AD等於劣弧BD，優弧ACO=優弧BCO
推論二：弦的垂直平分線經過圓心，並且平分這條弦所對的弧。
幾何語言：∵DC垂直AB，AE=EB
∴DC是圓的直徑，劣弧AD等於劣弧BD，優弧ACO=優弧BCO
推論三：平分弦所對的一條弧的直徑垂直平分這條弦，並且平分這條弦所對的另一條弧。
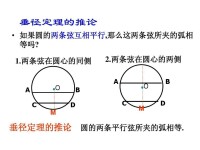
推論四：在同圓或者等圓中，兩條平行弦所夾的弧相等。
歐幾里得（古希臘數學家 希臘文：Ευκλειδης. ，公元前330年~公元前275年，）幾何原本第I卷中的第12個命題實際即為垂徑定理，這可能是最早的有關於垂徑定理的記載。
垂徑定理是圓的重要性質之一，它是證明圓內線段、角相等、垂直關係的重要依據，也為圓中的計算、證明和作圖提供了依據、思路和方法。
基本信息
- 中文名
- 垂徑定理
- 外文名
- Vertical theorem
- 提出時間
- 約前300年
- 別名
- 垂定
- 表達式
- 無
- 提出者
- 歐幾里得（Ευκλειδης）
- 應用學科
- 數學
- 適用領域
- 幾何，解析幾何，有圓的平面直角坐標系
- 影響
- 是圓的重要性質之一