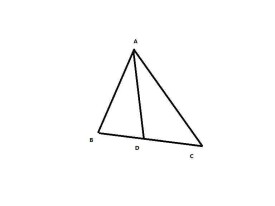
三角形的中線
連接頂點到對邊中點的線段
三角形中，連接一個頂點和它所對邊的中點的線段叫做三角形的中線。任何三角形都有三條中線，而且這三條中線都在三角形的內部，並交於一點。由定義可知，三角形的中線是一條線段。由於三角形有三條邊，所以一個三角形有三條中線，且三條中線交於一點。這點稱為三角形的重心。每條三角形中線分得的兩個三角形面積相等。
目錄
設△ABC的角A、B、C的對邊分別為a、b、c．
1、三角形的三條中線都在三角形內。
2、三角形的三條中線長：
ma=(1/2)√2b^2+2c^2-a² ；
mb=(1/2)√2c^2+2a^2-b^2 ；
mc=(1/2)√2a^2+2b^2-c^2 。
(ma,mb,mc分別為角A,B,C所對邊的中線長）
3、三角形的三條中線交於一點，該點叫做三角形的重心。
4、直角三角形斜邊上的中線等於斜邊的一半。
5.三角形中線組成的三角形面積等於這個三角形面積的3/4。
6.三角形重心將中線分為長度比為1:2的兩條線段。
基本信息
- 中文名
- 三角形的中線