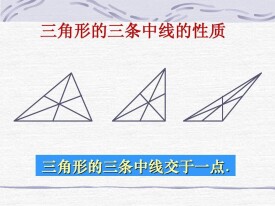
三角形中線
連接頂點和它所對邊中點的線段
三角形的中線是接三角形頂點和它的對邊中點的線段。每個三角形都有三條中線,它們都在三角形的內部。在三角形中,三條中線的交點是三角形的重心。三角形的三條中線交於一點,這點位於各中線的三分之二處。
設△ABC的角A、角B、角C的對邊分別為a、b、c.
1、三角形的三條中線都在三角形內。
2、三角形的三條中線長:
ma=(1/2)√2b²+2c²-a² ;
mb=(1/2)√2c²+2a²-b² ;
mc=(1/2)√2a²+2b²-c²。
(ma,mb,mc分別為角A,B,C所對邊的中線長)
3、三角形的三條中線交於一點,該點叫做三角形的重心。
4、直角三角形斜邊上的中線等於斜邊的一半。
5.三角形中線組成的三角形面積等於這個三角形面積的3/4。
6.三角形重心將中線分為長度比為1:2的兩條線段。
三角形中線組成的三角形面積等於這個三角形面積的3/4.
給出一個△ABC.中線為CD,BF,AE.(如右圖)
解:連接DE並延長到G,使EG=DE.連接BG,FG,EF.
在△DEC和△GEB中
∵DE=EG,∠BEG=∠DEC,BE=EC.
∴△DEC≌△GEB(SAS).
∴CD=BG. S△DEC=S△GEB.
又∵DE平行且等於1/2AC,DE=EG.
∴EG平行且等於1/2AC.
即EG平行且等於AF.
∴四邊形AEGF為平行四邊形(對邊平行且相等的四邊形為平行四邊形)
∴AE=FG . S△EFG =S△AEF.
這樣△ABC的三條中線CD,BF,AE就構成了△BFG.
∵BF為中線,平分△ABC面積.
∴S△BAF=S△BFC.
又∵EF為△BFC中線,平分△BFC面積.
∴S△BEF=S△EFC=1/4 S△ABC.
又∵CD為△ABC中線,平分△ABC面積.
∴S△ADC=S△BDC.
又∵DE平分△BDC面積.
∴S△BDE=S△DEC=1/4 S△ABC.
∴S△BEG=S△DEC=1/4 S△ABC.
∵AE為△ABC中線,平分△ABC面積.
∴S△BAE=S△AEC.
又∵EF平分△AEC.
∴S△AEF=S△EFC.
∴S△AFE=S△EFG=1/4 S△ABC
∵S△BFG =S△BEF+S△BEG +S△EFG
=1/4 S△ABC+1/4 S△ABC+1/4 S△ABC
=3/4 S△ABC
三形中任意兩條中線的和大於第三條中線
證明:由已知可得CD,BF, AE為△ABC的中線,P為△ABC的重心,∴AP=2/3 AE,CP=2/3 CD,PF=1/2 BP=1/3 BF(重心的性質),延長PF到M,使PF=FM,於是四邊形APCM為平行四邊形,∴AM=CP,△APM中:有AP+AM>PM ∴AP+CP>2PF,AP+CP>BP,2/3 AE+2/3 CD>2/3 BF,即AE+CD>BF 同理,AE+BF>CD,BF+CD>AE,所以得證:三角形中任意兩條中線的和大於第三條中線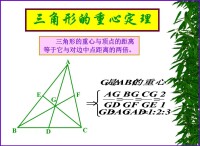

三角形的重心定理
而這兩個概念又存在著共同點:
1、都是線段;
2、每一個三角形都有三條中線,也都有三條中位線。
內心:三角形的內心是三角形三條內角平分線的交點。
外心:三角形三條邊的中垂線的交點叫作三角形的外心,即外接圓圓心。
重心:三角形三條中線的交點叫作三角形的重心。
垂心:三角形三條垂線的交點叫作三角形的垂心。
如圖所示, BF,CD,AE分別為 正三角形ABC的三條高,中線,角平分線,其 交點P即為 正三角形ABC的 中心。
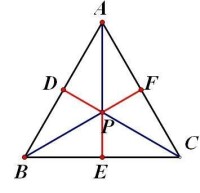
三角形中線