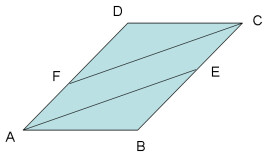
平行四邊形
兩組對邊分別平行的四邊形
平行四邊形,是在同一個二維平面內,由兩組平行線段組成的閉合圖形。平行四邊形一般用圖形名稱加四個頂點依次命名。註:在用字母表示四邊形時,一定要按順時針或逆時針方向註明各頂點。
在歐幾里德幾何中,平行四邊形是具有兩對平行邊的簡單(非自相交)四邊形。平行四邊形的相對或相對的側面具有相同的長度,並且平行四邊形的相反的角度是相等的。
相比之下,只有一對平行邊的四邊形是梯形。平行四邊形的三維對應是平行六面體。
兩組對邊分別平行的四邊形叫做平行四邊形。
1.平行四邊形屬於平面圖形。
2.平行四邊形屬於四邊形。
3.平行四邊形屬於中心對稱圖形。
(矩形、菱形、正方形都是特殊的平行四邊形。)
(1)如果一個四邊形是平行四邊形,那麼這個四邊形的兩組對邊分別相等。
(簡述為“平行四邊形的兩組對邊分別相等”)
(2)如果一個四邊形是平行四邊形,那麼這個四邊形的兩組對角分別相等。
(簡述為“平行四邊形的兩組對角分別相等”)
(3)如果一個四邊形是平行四邊形,那麼這個四邊形的鄰角互補。
(簡述為“平行四邊形的鄰角互補”)
(4)夾在兩條平行線間的平行的高相等。(簡述為“平行線間的高距離處處相等”)
(5)如果一個四邊形是平行四邊形,那麼這個四邊形的兩條對角線互相平分。
(簡述為“平行四邊形的對角線互相平分”)
(6)連接任意四邊形各邊的中點所得圖形是平行四邊形。(推論)
(7)平行四邊形的面積等於底和高的積。(可視為矩形。)
(8)過平行四邊形對角線交點的直線,將平行四邊形分成全等的兩部分圖形。
(9)平行四邊形是中心對稱圖形,對稱中心是兩對角線的交點.
(10)平行四邊形不是軸對稱圖形,但平行四邊形是中心對稱圖形。矩形和菱形是軸對稱圖形。註:正方形,矩形以及菱形也是一種特殊的平行四邊形,三者具有平行四邊形的性質。
(11)平行四邊形ABCD中(如圖)E為AB的中點,則AC和DE互相三等分,一般地,若E為AB上靠近A的n等分點,則AC和DE互相()等分。
(12)平行四邊形ABCD中,AC、BD是平行四邊形ABCD的對角線,則各四邊的平方和等於對角線的平方和。
(13)平行四邊形對角線把平行四邊形面積分成四等份。
(14)平行四邊形中,兩條在不同對邊上的高所組成的夾角,較小的角等於平行四邊形中較小的角,較大的角等於平行四邊形中較大的角。
(15)平行四邊形的面積等於相鄰兩邊與其夾角正弦的乘積
平行四邊形的對邊是平行的(根據定義),因此永遠不會相交。
平行四邊形的面積是由其對角線之一創建的三角形的面積的兩倍。
平行四邊形的面積也等於兩個相鄰邊的矢量交叉乘積的大小。
任何通過平行四邊形中點的線將該區域平分。
任何非簡併仿射變換都採用平行四邊形的平行四邊形。
平行四邊形具有2階(至180°)的旋轉對稱性(如果是正方形則為4階)。如果它也具有兩行反射對稱性,那麼它必須是菱形或長方形(非矩形矩形)。如果它有四行反射對稱,它是一個正方形。
平行四邊形的周長為,其中a和b為相鄰邊的長度。
與任何其他凸多邊形不同,平行四邊形不能刻在任何小於其面積的兩倍的三角形。
在平行四邊形的內側或外部構造的四個正方形的中心是正方形的頂點。
如果與平行四邊形平行的兩條線與對角線并行構成,則在該對角線的相對側上形成的平行四邊形面積相等
平行四邊形的對角線將其分成四個相等面積的三角形。
● ● 兩組對邊分別平行的四邊形是平行四邊形(定義判定法);
● ● 一組對邊平行且相等的四邊形是平行四邊形;
● ● 兩組對邊分別相等的四邊形是平行四邊形;
● ● 兩組對角分別相等的四邊形是平行四邊形(兩組對邊平行判定);
● ● 對角線互相平分的四邊形是平行四邊形。補充:條件3僅在平面四邊形時成立,如果不是平面四邊形,即使是兩組對邊分別相等的四邊形,也不是平行四邊形。
一、連接對角線或平移對角線。
二、過頂點作對邊的垂線構成直角三角形。
三、連接對角線交點與一邊中點,或過對角線交點作一邊的平行線,構成線段平行或中位線。
四、連接頂點與對邊上一點的線段或延長這條線段,構造相似三角形或等積三角形。
五、過頂點作對角線的垂線,構成線段平行或三角形全等。
1、(1)平行四邊形的面積公式:(可運用割補法,推導方法如圖);如用“h”表示高,“a”表示底,“S”表示平行四邊形面積,則。
(2)平行四邊形的面積等於兩組鄰邊的積乘以夾角的正弦值;如用“a”“b”表示兩組鄰邊長,α表示兩邊的夾角,“S”表示平行四邊形的面積,則。
2、平行四邊形周長:四邊之和。可以二乘(底1+底2);如用“a”表示底1,“b”表示底2,“c平”表示平行四邊形周長,則平行四邊的周長。
定義:有一個角是直角的平行四邊形是矩形。
判定:
1.有一個角是直角的平行四邊形是矩形;
2.對角線相等的平行四邊形是矩形;
3.有三個角是直角的四邊形是矩形;
4.對角線相等且互相平分的四邊形是矩形。
性質:
1.矩形具有平行四邊形的一切性質;
2.矩形的對角線相等;
3.矩形的四個角都是90度;
4.矩形是軸對稱圖形,又是中心對稱圖形.它有2條對稱軸,分別是每組對邊中點連線所在的直線;對稱中心是兩條對角線的交點。
定義:有一組鄰邊相等的平行四邊形是菱形。
判定:
1.一組鄰邊相等的平行四邊形是菱形;
2.對角線互相垂直的平行四邊形是菱形;
3.四邊相等的四邊形是菱形。
性質:
1.菱形具有平行四邊形的一切性質;
2.菱形四邊相等;
3.菱形每條對角線平分一組對角;
4.菱形是中心對稱圖形,也是軸對稱圖形。
定義:一組鄰邊相等且有一個角是直角的平行四邊形是正方形。
判定:
1.一組鄰邊相等的矩形是正方形;
2.有一個角是直角的菱形是正方形;
3.對角線互相垂直的矩形是正方形;
4.對角線相等的菱形是正方形。
性質:
正方形具有矩形和菱形的一切性質。
1.用邊長分別為50cm,75cm,100cm的兩個全等三角形拼成四邊形,共能拼成_________個四邊形,___________個為平行四邊形。
2.在四邊形ABCD中,若,再添加一個條件為__________,就可以判定四邊形ABCD為平行四邊形。
3.延長的中線AD至E,使,連接BE,CE,則AB_________CE,AC_________BE。
4.若四邊形ABCD中,AC,BD相交於點O,要判定它為平行四邊形,從角的關係看應滿足____對角相等_______,從對角線的關係看應滿足______對角線互相平分_________。
5.已知E、F、G、H分別為ABCD各邊的中點,則四邊形EFGH為_______________。
二、選一選
6.能識別四邊形ABCD是平行四邊形的題設是( )
A.
B.
C.
D.
7.點A,B,C,D在同一平面內,從①,②,③,④這四個條件中任選兩個,能使四邊形ABCD是平行四邊形的選法有()
A.3種 B.4種 C.5種 D.6種
8.下列結論正確的是( )
A.對角線相等且一組對角相等的四邊形是平行四邊形
B.一邊長為125cm,兩條對角線長分別是100cm和150cm的四邊形是平行四邊形
C.一組對邊平行且一組對角相等的四邊形是平行四邊形
D.對角線相等的四邊形是平行四邊形
9.不能判定四邊形ABCD是平行四邊形的條件是()
A.
B.
C.
D.
10.如圖19-1-26,在ABCD中,E,F分別在BC,AD上,若想使四邊形AFCE為平行四邊形,須添加一個條件,這個條件可以是( )。
①;②;③;④。
A.①或② B.②或③ C.③或④ D.①或③或④
11.如圖19-1-27,在中,,,,則下列說法中正確的有( )個。
①圖中共有三個平行四邊形;
②;
③;
④圖中共有三對全等三角形。
A.1 B.2 C.3 D.4
三、解答題
12.如圖19-1-28,在ABCD中,E,F為BD上的點,,那麼四邊形AECF是什麼圖形?試用兩種方法證明。
13.已知:在中,,EF是的中位線,分別交AB,AC於E,F,延長AB到D,使,連接CD。求證:。
14.如圖19-1-29,ABCD中,對角線AC、BD相交於點O,過點O作兩條直線分別與AB,BC,CD,AD交於G,F,H,E四點。求證:四邊形EGFH是平行四邊形。
15.如圖19-1-30,分別以的三邊為邊長,在BC的同側作等邊三角形ABD,等邊三角形BCE,等邊三角形ACF,連接DE,EF。求證:四邊形ADEF是平行四邊形。
四、思維拓展
16.如圖19-1-31,在ABCD中,,,垂足分別為點E,F,點G,H分別為AD,BC的中點,試證明EF和GH互相平分。
17.如圖19-1-32,是邊長為100px的邊三角形,P是內的任意一點,過點P作分別交AC,BC於點E,F,作分別交AB,AC於點G,H,作分別交AB,BC於點M,N,試猜想:的值是多少?其值是否隨P位置的改變而變化?並說明你的理由。
五、中考熱身
18.(2005年蘇州市)如圖19-1-33,在ABCD中,下列各式不一定正確的是( )。
A.
B.
C.
D.
答案:
1.六;三。2.或。3.= ; =4.,,
;,5.平行四邊形
6.C 7.B 8.C 9.C 10.D 11.B
12.平行四邊形。方法一:連接AC,利用“對角線互相平分的四邊形為平行四邊形”來證明。
方法二:證,,利用“兩組對邊分別相等的四邊形為平行四邊形”來證明。
13.提示:先證明,得,再證。
14.先證,得,同理可得,所以四邊形EGFH是平行四邊形。
15.先證,可得,。,四邊形ADEF是平行四邊形。
16.提示:連接GE,EH,HF,GF,先證,再證即可。
17.其值為200px,且不隨P位置的改變而變化。
理由:由為等邊三角形可得也是等邊三角形,
①,
同理,也為等邊三角形,
。②
,
四邊形AMPE為平行四邊形,
,同理,BFPG也為平行四邊形,
,
。③
①+②+③得。
18.D