面積公式
計算一個圖形的面積的一般通用方法
1. 一個圖形的面積等於它的各部分面積的和;
2. 兩個全等圖形的面積相等;
3. 等底等高的三角形、平行四邊形、梯形(梯形等底應理解為兩底的和相等)的面積相等;
4. 等底(或等高)的三角形、平行四邊形、梯形的面積比等於其所對應的高(或底)的比;
5. 相似三角形的面積比等於相似比的平方;
6. 等角或補角的三角形面積的比,等於夾等角或補角的兩邊的乘積的比;等角的平行四邊形面積比等於夾等角的兩邊乘積的比;
7. 任何一條曲線都可以用一個函數來表示,那麼,這條曲線所圍成的面積就是對X求積分。
設圓半徑為r,面積為S,則面積(π 表示圓周率)。即圓面積等於圓周率乘以圓半徑的平方。
在半徑為R的圓中,因為360°的圓心角所對的扇形的面積就是圓面積,所以圓心角為n°的扇形面積:
比如:半徑為1cm的圓,那麼所對圓心角為135°的扇形的周長:
扇形的面積:
扇形還有另一個面積公式:,其中l為弧長,R為半徑。
圓環周長:外圓的周長+內圓的周長(圓周率X(大直徑+小直徑))圓環面積:外圓面積-內圓面積(圓周率X大半徑的平方-圓周率X小半徑的平方\圓周率X(大半徑的平方-小半徑的平方)
用字母表示:
還有第二種方法:
R=大圓半徑
r=圓環寬度=大圓半徑-小圓半徑
還有一種方法:
已知圓環的外直徑為D,圓環厚度(即外內半徑之差)為d。
,可由第一、二種方法推得,圓環面積。
這是根據外直徑和圓環厚度(即外內半徑之差)得出面積。這兩個數據在現實易於測量,適用於計算實物,例如圓鋼管。
任意三角形的面積公式(海倫公式):,, a,b,c為三角形三邊。
1:三頂點的坐標分別為
。
2:空間,三頂點的坐標分別為,面積為S,則
。
設弓形AB所對的弧為弧AB,那麼:
當弧AB是劣弧時,那麼(A、B是弧的端點,O是圓心)。
當弧AB是半圓時,那麼。
當弧AB是優弧時,那麼(A、B是弧的端點,O是圓心)
計算公式分別是:
,
,
。
橢圓面積公式: 橢圓面積定理:橢圓的面積等於圓周率(π)乘該橢圓長半軸長(a)與短半軸長(b)的乘積。
橢圓面積公式應用實例
橢圓的長半軸為8cm,短半軸為6cm,假設π=3.14,求該橢圓的面積。
答:
定理簡述及證明
菱形面積=對角線乘積的一半,即
菱形的面積也可=底乘高
拋物線弓形面積公式等於:以割線為底,以平行於底的切線的切點為頂點的內接三角形的,即:
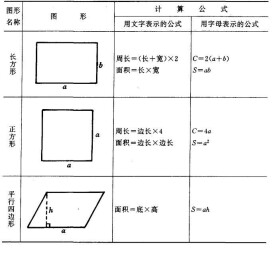
長方形由長與寬構成,其面積公式為,其中S為長方形面積,a為長方形的長,b為長方形的寬。
正方形由四條邊構成,四條邊相等,其面積公式為,其中S為正方形面積,a為正方形邊長。
平行四邊形是由兩組平行線段組成的閉合圖形。其面積公式為,其中S為平行四邊形面積,a為平行四邊形的底長,h為平行四邊形的高。