全等三角形
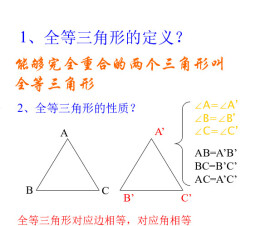
能夠完全重合的兩個三角形
經過翻轉、平移后，能夠完全重合的兩個三角形叫做全等三角形，而該兩個三角形的三條邊及三個角都對應相等。全等三角形指兩個全等的三角形，它們的三條邊及三個角都對應相等。全等三角形是幾何中全等之一。根據全等轉換，兩個全等三角形經過平移、旋轉、翻折后，仍舊全等。正常來說，驗證兩個全等三角形一般用邊邊邊（SSS）、邊角邊（SAS）、角邊角（ASA）、角角邊（AAS）、和直角三角形的斜邊，直角邊（HL）來判定。
1．全等三角形的對應角相等。
2．全等三角形的對應邊相等。
3. 能夠完全重合的頂點叫對應頂點。
4．全等三角形的對應邊上的高對應相等。
5．全等三角形的對應角的角平分線相等。
6．全等三角形的對應邊上的中線相等。
7．全等三角形面積和周長相等。
8．全等三角形的對應角的三角函數值相等。
在第一行寫要進行判定全等的兩個三角形；
第二行畫大括弧，分別寫判定的三個條件，並註明理由；
在第三行寫出結論，並說明理由。
1.公共邊；2.已知；3.已證；4.公共角；5.由定義推到的角，如“對頂角相等”。
最後一行，寫兩個三角形全等並註明理由.（如圖）
（若為直角三角形，在第二行須先寫明兩個直角相等並為90度，再寫兩個斜邊、直角邊分別相等）。
全等三角形
（例：Rt△xxx與Rt△xxx）
（提示：線段的垂直平分線上的一點到線段的兩個端點的距離相等）
三個角對應相等的兩個三角形不一定全等，兩邊和其中一邊的對角對應相等的兩個三角形也不一定全等。
● SSS（Side-Side-Side）（邊邊邊）：三邊對應相等的三角形是全等三角形。
● SAS（Side-Angle-Side）（邊角邊）：兩邊及其夾角對應相等的三角形是全等三角形。
● ASA（Angle-Side-Angle）（角邊角）：兩角及其夾邊對應相等的三角形全等。
● AAS（Angle-Angle-Side）（角角邊）：兩角及其一角的對邊對應相等的三角形全等。
● RHS（Right angle-Hypotenuse-Side）（直角、斜邊、邊）（又稱HL定理(斜邊、直角邊)）：在一對直角三角形中，斜邊及另一條直角邊相等。（它的證明是用SSS原理）
下列兩種方法不能驗證為全等三角形：
● AAA（Angle-Angle-Angle）（角角角）：三角相等，不能證全等，但能證相似三角形。
● SSA（Side-Side-Angle）（邊邊角）：其中一角相等，且非夾角的兩邊相等。
不能驗證全等三角形的判定
全等三角形
這樣，便能得知若邊無限地根據比例加長，角度都保持不變。因此，AAA並不能判定全等三角形。
但在球面幾何上，AAA可以判定全等三角形（運用三角形與其極對稱三角形的邊角關係證明），而AAS不能判定全等三角形（球面三角形內角和大於180°）。
SSS（邊邊邊）
即三邊對應相等的兩個三角形全等.
舉例：如下圖，，求證.
證明：在△ACD與△BDC中{.（SSS）
.（全等三角形的對應角相等）
SAS（邊角邊）
即三角形的其中兩條邊對應相等，且兩條邊的夾角也對應相等的兩個三角形全等.
舉例：如下圖，AB平分∠CAD，，求證.
證明：∵AB平分∠CAD.
.
在△ACB與△ADB中{.
.（SAS）
.（全等三角形的對應角相等）
ASA（角邊角）
即三角形的其中兩個角對應相等，且兩個角夾邊也對應相等的兩個三角形全等.
舉例：如下圖，，，求證.
證明：在△ABE與△ACD中{.
.（ASA）
AAS（角角邊）
即三角形的其中兩個角對應相等，且對應相等的角所對應的邊也對應相等的兩個三角形全等.
舉例：如下圖，，，求證.
證明：在△ABC與△EDC中{.
.（AAS）
.（全等三角形的對應角相等）
HL（斜邊、直角邊）
舉例：如下圖，Rt△ADC與Rt△BCD，，求證.
證明：在Rt△ADC與Rt△BCD中{.
.（HL）
.（全等三角形的對應邊相等）
用途
因為多邊形可由多個三角形組成，所以利用此方法，亦可驗證其它全等的多邊形。
利用性質和判定，學會準確地找出兩個全等三角形中的對應邊與對應角是關要驗證全等三角形，不需驗證所有邊及所有角也對應地相同。以下判定，是由三個對應的部分組成，即全等三角形可透過以下定義來判定：
SSS（Side-Side-Side）（邊、邊、邊）：各三角形的三條邊的長度都對應相等的話，該兩個三角形就是全等三角形。
SAS（Side-Angle-Side）（邊、角、邊）：各三角形的其中兩條邊的長度都對應相等，且這兩條邊的夾角（即這兩條邊組成的角）都對應相等的話，該兩個三角形就是全等三角形。
ASA（Angle-Side-Angle）（角、邊、角）：各三角形的其中兩個角都對應相等，且這兩個角的夾邊（即公共邊，）都對應相等的話，該兩個三角形就是全等三角形。
AAS（Angle-Angle-Side）（角、角、邊）：各三角形的其中兩個角都對應相等，且其中一個角的對邊（三角形內除組成這個角的兩邊以外的那條邊）或鄰邊（即組成這個角的一條邊）對應相等的話，該兩個三角形就是全等三角形。
HL定理（hypotenuse -leg） （斜邊、直角邊）：直角三角形中一條斜邊和一條直角邊都對應相等，該兩個三角形就是全等三角形。
1.性質中三角形全等是條件，結論是對應角、對應邊相等。在寫兩個三角形全等時，一定把對應的頂點，角、邊的順序寫一致，為找對應邊，角提供方便。
2.當圖中出現兩個以上等邊三角形時，應首先考慮用SAS找全等三角形。
3.用在實際中，一般我們用全等三角形測相等的距離。以及相等的角，可以用於工業和軍事。
4.三角形具有一定的穩定性，所以我們用這個原理來做腳手架及其他支撐物體。
一般來說線段和角相等需要證明全等。
因此我們可以來採取逆向思維的方式。
來想要證全等，則需要什麼條件
要證某某邊等於某某邊，那麼首先要證明含有那兩個邊的三角形全等。
全等三角形
有時還需要畫輔助線幫助解題。常用的輔助線有：中線倍長，截長補短等。
分析完畢以後要注意書寫格式，在全等三角形中，如果格式不寫好那麼就容易出現看漏的現象。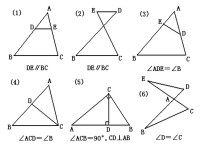
全等三角形
基本信息
- 中文名
- 全等三角形
- 外文名
- congruent triangles
- 出處
- 數學
- 判定
- SSS SAS ASA等
- 性質
- 三邊三角相等
- 屬於
- 幾何全等