垂心

垂心是從三角形的各個頂點向其對邊所作的三條垂線的交點。

銳角三角形垂心在三角形內部。

直角三角形垂心在三角形直角頂點。

鈍角三角形垂心在三角形外部。

三角形三個頂點，三個垂足，垂心這7個點可以得到6組四點共圓。

三角形上作三高，三高必於垂心交。

高線分割三角形，出現直角三對整，

直角三角有十二，構成九對相似形，

四點共圓圖中有，細心分析可找清。

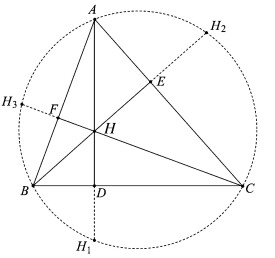
設的三條高為AD、BE、CF，其中D、E、F為垂足，垂心為H，角A、B、C的對邊分別為a、b、c，．

1、銳角三角形的垂心在三角形內；直角三角形的垂心在直角頂點上；鈍角三角形的垂心在三角形外.

2、三角形的垂心是它垂足三角形的內心；或者說，三角形的內心是它旁心三角形的垂心；

3、垂心H關於三邊的對稱點，均在△ABC的外接圓上。

4、中，有六組四點共圓，有三組(每組四個)相似的直角三角形，且。

5、H、A、B、C四點中任一點是其餘三點為頂點的三角形的垂心(並稱這樣的四點為一—垂心組)。

6、，，，的外接圓是等圓。

7、在非直角三角形中，過H的直線交AB、AC所在直線分別於P、Q，則。

8、設O，H分別為的外心和垂心，則，，。

9、銳角三角形的垂心到三頂點的距離之和等於其內切圓與外接圓半徑之和的2倍。

10、銳角三角形的垂心是垂足三角形的內心；銳角三角形的內接三角形(頂點在原三角形的邊上)中，以垂足三角形的周長最短（施瓦爾茲三角形，最早在古希臘時期由海倫發現）。

11、西姆松定理（西姆松線）：從一點向三角形的三邊所引垂線的垂足共線的充要條件是該點落在三角形的外接圓上。

12、設銳角△ABC內有一點P，那麼P是垂心的充分必要條件是。

13、設H為非直角三角形的垂心，且D、E、F分別為H在BC，CA，AB上的射影，分別為，，的垂心，則。

14、三角形垂心H的垂足三角形的三邊，分別平行於原三角形外接圓在各頂點的切線。

15、三角形任一頂點到垂心的距離，等於外心到對邊的距離的2倍。（垂心伴隨外接圓，必有平行四邊形）

推論（垂心餘弦定理）：銳角三角形ABC的垂心為H，則（可引入有向距，推廣到任意三角形）

16、等邊三角形的垂心把三角形的高分成2:1兩段，靠近頂點的那段長度為高的三分之二。(高中學習中常用知識）

證明：

如圖：

作於點E,於點F,且BE交CF於點H,連接AH並延長交BC於點D.現在我們只要證明即可.

因為

所以四邊形BFEC為圓內接四邊形.

四邊形AFHE為圓內接四邊形.

所以

由得

四邊形AFDC為圓內接四邊形

所以

即

設點H為銳角三角形ABC的垂心，向量，向量，向量，向量，

則

垂心坐標的解析解：

設三個頂點的坐標分別為，那麼垂心坐標

其中，

垂心的向量特徵：三角形ABC內一點O，向量，則點O是三角形的垂心

證明

由OA·OB=OB·OC，得

OA·OB-OC·OB=0

∴(OA-OC)·OB=0

∴CA·OB=0，即OB垂直於AC邊

同理由OB·OC=OC·OA，可得OC垂直於AB邊

由OA·OB=OC·OA，得OA垂直於BC邊

∴點O是三角形的垂心。