曲邊三角形

curved edge triangle，又稱魯洛三角形Reuleaux triangle。

曲邊三角形的畫法如下:

1．畫一個等邊三角形；

2．以所作的等邊三角形的三個頂點為圓心，邊長為半徑，作各內角所對的圓弧。

等寬曲線

顯然，這個等寬曲線的寬度等於原來等邊三角形的邊長。請你親自動手做個實驗。把一硬紙卡片剪出一個如上所畫的等寬曲線的樣子，而用另一硬紙卡片剪下一個正方形的洞。如果正方形的邊長等於曲線的寬度，那麼不管方向怎樣變化，它正好合適地裝入這個曲線板，並且這個等寬曲線板可以在正方形內緊密無間地自由轉動。實際上，任何等寬曲線都可以在邊長等於曲線寬度的正方形內緊密無間而自由地轉動；反之，可以在正方形內緊密而自由地轉動的曲線也是等寬曲線。

用這種等寬曲線做橫斷面的滾子，也能使載重物水平地移動，而不至於上下顛簸。這種具有奇特功能的曲邊三角形，是由工藝學家魯洛首先發現的，所以也稱為魯洛曲邊三角形。

在魯洛的等寬曲線上有尖點，即在兩條圓弧相交處形成角頂。我們希望它光滑一些，可以按下面的方法得到沒有任何角頂的新的等寬曲線：把等邊三角形的各邊向兩個方向延長相等的一段；以三個頂點為圓心畫圓弧，使得三個內角所對的圓弧的半徑，等於邊長與延長線的長度的和；內角的對頂角所對的圓弧，等於延長線的長。由這樣的六條圓弧組成的等寬曲線克服了尖點，因此光滑得多了。

畫等寬曲線的關鍵的想法是

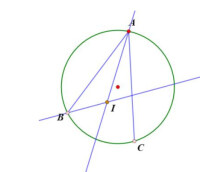
圓弧的中心是它所對的角頂。下面介紹一種等寬的曲邊多邊形的一般畫法，並使它的寬度為b。開始可以把任意點B作為第一個角頂，以B為圓心、b為半徑畫弧；在這個弧上，選擇A和C二點作為新角頂，以C為圓心、b為半徑畫弧（該弧必經過B）；在這個弧上，選擇另一個角頂D，以D為圓心、b為半徑畫弧（該弧必經過C），如果我們希望結束這個過程，可以在這個弧上選擇角頂E，使它也處在以A為圓心、b為半徑的弧上（該弧必經過點B）。也就是E是兩個弧的交點。最後，用一個以E為圓心、b為半徑的弧連接A和D，這樣就得到一個等寬的曲邊五邊形ADBEC（如圖6）。邊數更多的多邊形，可用同樣的方法作出來，這隻要多作幾步，然後使曲線成為閉合的就可以了。

同樣的原理，我們還可以利用這些曲線得到沒有任何角頂的等寬曲線。

這些方法使我們可以構作無數個等寬曲線，它們都是由許多圓弧組成的。但不要誤解為等寬曲線只能由圓弧組成，實際上有這樣的等寬曲線，它的一部分不管是多麼小，都不是圓弧。在這裡我們不可能介紹它，因為已經超出了初中幾何知識的範圍。

日常生活中，我們看到許多加蓋的盛具，如鍋、杯、壺、缸、桶之類，都是圓口圓蓋的形狀。這除了容易加工製造以外，主要還是應用圓是等寬曲線的特性。圓形的蓋子，只要它不變形，從任何方向都不會掉進盛具里去。為了提高觀賞價值與品茶雅興，一些藝術茶壺的壺蓋可以設計成其他等寬曲線的形狀。

實際上這就是等寬曲線，為了方便大家的搜索，增加了此詞條。

三角剖分是代數拓撲學里最基本的研究方法。以曲面為例，我們把曲面剖開成一塊塊碎片，要求滿足下麵條件：

（1）每塊碎片都是曲邊三角形

（2）曲面上任何兩個這樣的曲邊三角形，要麼不相交，要麼恰好相交於一條公共邊（不能同時交兩條或兩條以上的邊）

拓撲學的一個已知事實告訴我們：任何曲面都存在三角剖分。

假設曲面上有一個三角剖分，我們把所有三角形的頂點總個數記為p(公共頂點只看成一個，下同),邊數記為l,三角形的個數記為n,則是曲面的拓撲不變數！也就是說不管是什麼剖分， e總是得到相同的數值。 e被稱為稱為歐拉示性數。

假設g是曲面上洞眼的個數（比如球面沒有洞，故;又如環面有一個洞，故），那麼。

g也是拓撲不變數，稱為曲面的虧格(genus)。

上面例舉曲面的情形。對一般的拓撲對象（復形），我們有類似的剖分，通常成為單純剖分。分割出的每塊碎片稱為單純形（簡稱單形）