抽樣調查法
抽樣調查法
抽樣徠調查法是指從研究對象的全部單位中抽取一部分單位進行考察和分析,並用這部分單位的數量特徵去推斷總體的數量特徵的一種調查方法。其中,被研究對象的全部單位稱為“總體”;從總體中抽取出來,實際進行調查研究的那部分對象所構成的群體稱為“樣本”。在抽樣調查中,樣本數的確定是一個關鍵問題。
按規模大小成比例的概率抽樣,簡稱為PPS抽樣,它是一種使用輔助信息,從而使每個單位均有按其規模大小成比例的被抽中概率的一種抽樣方式。其抽選樣本的方法有漢森·赫維茨方法、拉希里方法等。
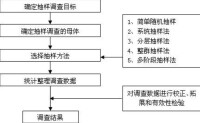
抽樣調查法流程圖
這是一種最簡單的一步抽樣法,它是從總體中選擇出抽樣單位,從總體中抽取的每個可能樣本均有同等被抽中的概率。抽樣時,處於抽樣總體中的抽樣單位被編排成1~n編碼,然後利用隨機數碼錶或專用的計算機程序確定處於1~n間的隨機數碼,那些在總體中與隨機數碼吻合的單位便成為隨機抽樣的樣本。
這種抽樣方法簡單,誤差分析較容易,但是需要樣本容量較多,適用於各個體之間差異較小的情況。
這種方法又稱順序抽樣法,是從隨機點開始在總體中按照一定的間隔(即“每隔第幾”的方式)抽取樣本。此法的優點是抽樣樣本分佈比較好,有好的理論,總體估計值容易計算。
它是根據某些特定的特徵,將總體分為同質、不相互重疊的若干層,再從各層中獨立抽取樣本,是一種不等概率抽樣。分層抽樣利用輔助信息分層,各層內應該同質,各層間差異儘可能大。這樣的分層抽樣能夠提高樣本的代表性、總體估計值的精度和抽樣方案的效率,抽樣的操作、管理比較方便。但是抽樣框較複雜,費用較高,誤差分析也較為複雜。此法適用於母體複雜、個體之間差異較大、數量較多的情況。
整群抽樣是先將總體單元分群,可以按照自然分群或按照需要分群,在交通調查中可以按照地理特徵進行分群,隨機選擇群體作為抽樣樣本,調查樣本群中的所有單元。整群抽樣樣本比較集中,可以降低調查費用。例如,在進行居民出行調查中,可以採用這種方法,以住宅區的不同將住戶分群,然後隨機選擇群體為抽取的樣本。此法優點是組織簡單,缺點是樣本代表性差。

統計學
多階段抽樣是採取兩個或多個連續階段抽取樣本的一種不等概率抽樣。對階段抽樣的單元是分級的,每個階段的抽樣單元在結構上也不同,多階段抽樣的樣本分佈集中,能夠節省時間和經費。調查的組織複雜,總體估計值的計算複雜。
抽樣的特點是總體中含量大的部分被抽中的概率也大,可以提高樣本的代表性。
抽樣的主要優點是:
(1)抽樣調查可以減少調查的工作量,調查內容可以求多、求全或求專,可以保證調查對象的完整性。
(2)可以從數量上以部分推算總體,利用概率論和數理統計原理,以一定的概率保證推算結果的可靠程度,起到全面調查認識總體的功能,可以保證調查的精度。
(3)因為抽樣調查是針對總體中的一部分單位進行的,抽樣調查可以大大減少調查費用,提高調查效率。
(4)收集、整理數據、綜合樣本的速度快,保證調查的時效性。
抽樣調查結果和真實值之間存在的差異稱為誤差。抽樣調查理論的中心任務之一,便是研究抽樣調查中的誤差。在抽樣調查誤差理論中將全部誤差分解為隨機誤差和系統誤差兩部分。隨機誤差是由於樣本與總體之間的隨機差異導致的,它存在於所有取樣過程中,是無法避免的,這種類型的誤差不會影響估計參數的均值,通常所計算的抽樣誤差就是這部分隨機誤差。對隨機誤差的研究,由於有強有力的概率論與數理統計理論和方法的支持,其理論已非常成熟,只要能設計出樣本估計量,就能給出相應估計量的隨機誤差公式。但是對抽樣調查中的系統誤差,由於導致系統性誤差的原因很多,而且多屬非隨機性因素,主要受主觀因素的影響,致使系統性誤差的出現是無規律的。構成系統誤差的因素有多種,大致可歸納為四種類型:
(1)設計誤差(Error in Design),是指因在抽樣調查方案設計過程中的錯誤而導致產生的系統性誤差。在抽樣方案徠的設計中,涉及抽樣框的編製、目標量和估計量的設計、樣本容量的確定和抽樣方式的選擇等,抽樣方案的設計還直接關係到在樣本的抽取過程中是否嚴格地遵循隨機性原則,若破壞了隨機性原則,必然會產生系統性誤差。
(2)估計量的偏誤(Bias of Estimator),是指所選擇的估計量(實則是估計方法)破壞了估計的優良標準之一——無偏性,致使產生統計性誤差。
(3)調查誤差(Error in Survey),是指在取得樣本數據資料過程中產生的誤差。這部分誤差通常與調查者、回答者、資料搜集方式和問卷等因素有關,它們會形成在調查過程中出現無回答和回答出現偏誤等情況,進而形成系統性誤差。
(4)編輯誤差(Processing in Error),是指在取得樣本資料之後,在整理、匯總、歸類、計算、錄入等過程形成的誤差。
因此,為了提高調查精度,一方面可以採取完善抽樣調查方案、合理選擇抽樣方法、提高抽樣調查數據的準確性、減少編輯誤差和調查誤差等手段,即減少系統誤差;另一方面要合理確定樣本量的大小,即減少隨機誤差。
通過對誤差分析可知,如果要提高調查的精度,一個重要方面就是確定合理的樣本量。樣本量大小的確定是一個平衡問題,如果在數據收集和分析過程採用大的樣本容量,達到給定研究目標和精度要求的費用就很高。太少的樣本則使結果受變異性的影響。
抽樣其具體的做法是:
1、首先確定初級抽樣單位(PSU),PSU可以是固定的常規單位,確定PSU需要有這些初級抽樣單位的具體名錄,以及每個初級抽樣單位中被調查人員的具體數目,這個數目可以的估計的人數。
2、確定抽取哪些初級抽樣單位,如果初級抽樣單位比較少,可以全部抽取,如果初級抽樣單位太多,則可以隨機抽取部分的抽樣單位。
3、在選取的初級抽樣單位中選擇具體的調查對象,如果將第二步中選取的初級抽樣單位的組成人員全部作為調查對象,稱為二階段整群抽樣,如果只是在初級抽樣單位中按人數的多少,來決定在每個抽樣單位中抽取多少人,則稱為PPS抽樣,此時,需要進行一定的計算,詳見有關統計書籍。
抽樣調查主要應用於以下幾個方面:
(1)某些總體本身的性質決定了不能對其進行全面調查而又要全面了解的情況,例如無限總體(連續生產產品的質量等)。
(2)某些總體理論上雖然可以全面調查,但實際上不可能也不必要的情況,例如調查城市居民出行情況。
(3)某些總體理論上雖然可以全面調查,但是實際上不可能的,例如破壞試驗(燈泡壽命、炮彈的殺傷力等)。
(4)某些特殊總體,要求具有相當資格的調查員才能進行,為此只能採用抽樣調查,例如對科學技術方面總體的調查。
(5)為了提高時效,要求在短時間內取得關於總體的情況。
(6)利用抽樣調查原理還可以對某總體的假設進行檢驗來判斷這種假設的真偽,以決定行動取捨。
抽樣調查是,一種非全面調查,它是從全部調查研究對象中,抽選一部分單位進行調查,並據以對全部調查研究對象作出估計和推斷的一種調查方法。顯然,抽樣調查雖然是非全面調查,但它的目的卻在於取得反映總體情況的信息資料,因而,也可起到全面調查的作用。根據抽選樣本的方法,抽樣調查可以分為概率抽樣和非概率抽樣兩類。概率抽樣是按照概率論和數理統計的原理從調查研究的總體中,根據隨機原則來抽選樣本,並從數量上對總體的某些特徵作出估計推斷,對推斷出可能出現的誤差可以從概率意義上加以控制。習慣上將概率抽樣稱為抽樣調查。
統計學(statistics)是應用數學的一個分支,主要通過利用概率論建立數學模型,收集所觀察系統的數據,進行量化的分析、總結,並進而進行推斷和預測,為相關決策提供依據和參考。它被廣泛的應用在各門學科之上,從物理和社會科學到人文科學,甚至被用來工商業及政府的情報決策之上。
