力矩分配法
計算超靜定結構的方法
力矩分配法(moment distribution method)力矩分配法是一種逐次逼近精確解的計算超靜定結構的方法。用一般的力法或位移法分析超靜定結構(見桿繫結構的靜力分析)時,都要建立和解算線性方程組。如果未知數目較多,計算工作將相當繁重。H.克羅斯於1930年在位移法的基礎上,提出了不必解方程組而是逐次逼近的力矩分配法。
以位移法為基礎的一種數值漸近方法,是美國H.克羅斯於1932年發表的,主要用於桿系剛結結構(如連續梁和剛架)的受力分析。
設想將結構承載后能產生位移的節點(桿件的連接點)用相應的假想約束固定,在假想約束處就產生不平衡力矩(或力),然後逐個放鬆附加約束,消除不平衡力矩(或力),恢復真實變形狀態。若首先放鬆節點i的附加約束,則i點的不平衡力矩就會使剛結於點的所有桿件變形,不平衡力矩隨即消失,這就是把分配給節點i備桿件的近端,而各桿件遠端由於受到i端分配力矩的影響也得到一定的力矩,前者稱為分配力矩,後者稱為傳遞力矩。然後再將節點固定住。在消除同節點i相鄰的節點j的不平衡力矩時,節點i得到了節點端傳來的力矩,以此作為i節點新的不平衡力矩,再次放鬆約束,將不平衡力矩分配給節點i各桿的近端。如此循環進行,直到各點不平衡力矩都趨於零為止。循環中,節點處第個桿的分配力矩為,其中分配係數,為第個桿的彎曲剛度,表示連接於節點處所有桿的彎曲剛度的總和。第個桿在端分配到的力矩對遠端(即節點k)的影響就是傳遞力矩,它等於,其中稱為傳遞係數,其值為:當,端鉸接,當 ,當端固定。循環計算完畢后,將各桿端各次的分配力矩、傳遞力矩和最初的不平衡力矩(稱為固端力矩)相加,即得各桿端的實際力矩值。此法適用於計算連續粱和無側移剛架。
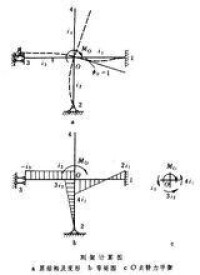
力矩分配法
有關。各桿的傳遞係數分別為。
根據靜力平衡原理,應等於各近端彎矩之和,即,如圖c。桿端發生單位轉角時的近端彎矩稱為該桿的轉動剛度,各桿轉動剛度之和 稱為結點 的轉動剛度。圖中任一桿的近端彎矩可表
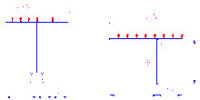
力矩分配法
因子稱為分配係數。它表明當點受到作用時,桿所分配到的力矩與該桿轉動剛度對結點轉動剛的比值有關。由此可知,點 受任一確定的外力矩作用時,任一桿的近端彎矩為;遠端彎矩為。
①固定結點,在結點O上加一剛臂控制轉動,分別求出各桿端由荷載產生的固端彎矩,作用於一結點上的各桿固端彎矩的代數和稱為不平衡力矩;
②放鬆結點,取消本不存在的剛臂,讓結點轉動,將不平衡力矩按各桿的分配係數求得各桿的分配力矩;
③傳遞力矩,按分配力矩和各桿的傳遞係數向各桿遠端傳遞,得各傳遞力矩。循此規則,分配、傳遞、反覆計算,直至得到足夠精度的桿端力矩數值為止。
最後,桿端力矩等於固端力矩、分配力矩、傳遞力矩之和。
對於有側移剛架,也可以應用由力矩分配法發展出來的方法計算,如無剪力分配法計算單跨剛架、附加剪力平衡方程的力矩分配法等,但其應用範圍受到限制或不很方便,所以對於一般有側移剛架,常採用迭代法。

力矩分配法
