位移法
位移法
以廣義位移(線位移和角位移)為未知量,求解固體力學問題的一種方法。位移法的思想是法國的C.-L.-M.-H.納維於1826年提出的。
位移法是解決超靜定結構最基本的計算方法,計算時與結構超靜定次數關係不大,相較於力法及力矩分配法,其計算過程更加簡單,計算結果更加精確,應用的範圍也更加廣泛,可以應用於有側移剛架結構的計算。此外,對於結構較為特殊的體系,應用位移法可以很方便地得出彎矩圖的形狀,位移法不僅適用於超靜定結構內力計算,也適用於靜定結構內力計算,所以學習和掌握位移法是非常有必要的。
簡單的來說:位移法就是把所有桿件變為三類基本構件的過程。在建立關於位移的平衡方程來解各個桿件的桿端位移。
以廣義位移(線位移和角位移)為未知量,求解固體力學問題的一種方法。位移法是計算超靜定結構的另一種基本的、也是有效的方法。不僅如此,對於靜定結構,位移法也是一種計算方法。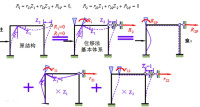

位移法
位移法可按兩種思路求解結點位移和桿端彎矩:典型方程法和平衡方程法。下面給出典型方程法的解題思路和解題步驟。
1、位移法典型方程的建立:
欲用位移法求解圖a所示結構,先選圖b為基本體系。然後,使基本體系發生與原結構相同的結點位移,受相同的荷載,又因原結構中無附加約束,故基本體系的附加約束中的約束反力(矩)必須為零,即:R1=0,R2=0。
而Ri是基本體系在結點位移Z1,Z2和荷載共同作用下產生的第i個附加約束中的反力(矩),按疊加原理Ri也等於各個因素分別作用時(如圖c,d,e所示)產生的第i個附加約束中的反力(矩)之和。於是得到位移法典型方程:
注意:
1.位移法方程的物理意義:基本體系在荷載等外因和各結點位移共同作用下產生的附加約束中的反力(矩)等於零。實質上是原結構應滿足的平衡條件。
2.位移法典型方程中每一項都是基本體系附加約束中的反力(矩)。其中:RiP表示基本體系在荷載作用下產生的第i個附加約束中的反力(矩);稱為自由項。rijZj表示基本體系在Zj作用下產生的第i個附加約束中的反力(矩);
3.主係數rii表示基本體系在Zi=1作用下產生的第i個附加約束中的反力(矩);rii恆大於零;
4.付係數rij表示基本體系在Zj=1作用下產生的第i個附加約束中的反力(矩);根據反力互等定理有rij=rji,付係數可大於零、等於零或小於零。
5.由於位移法的主要計算過程是建立方程求解方程,而位移法方程是平衡條件,所以位移法校核的重點是平衡條件(剛結點的力矩平衡和截面的投影平衡)。
2、求解步驟:
①確定位移法基本未知量,加入附加約束,取位移法基本體系。
②令附加約束髮生與原結構相同的結點位移,根據基本結構在荷載等外因和結點位移共同作用下產生的附加約束中的總反力(矩)=0,列位移法典型方程。
③繪出單位彎矩圖、荷載彎矩圖,利用平衡條件求係數和自由項。
④解方程,求出結點位移。
⑤用公式疊加最後彎矩圖。並校核平衡條件。
⑥根據M圖由桿件平衡求Q,繪Q圖,再根據Q圖由結點投影平衡求N,繪N圖。
1、截面直桿的轉角位移方程
各種因素共同作用下桿端彎矩的表達式稱為轉角位移方程。
①兩端固定梁轉角位移方程:
②一端固定一端鉸支梁轉角位移方程:
③一端固定一端定向支承梁轉角位移方程:
④已知桿端彎矩,可由桿件的矩平衡方程求出剪力:
其中是相應的簡支梁在荷載作用下的桿端剪力;MAB,MBA的正負按位移法規定。
2、直接列平衡方程法:
位移法方程實質上是靜力平衡方程。對於結點角位移,相應的是結點的力矩平衡方程;對於結點線位移,相應的是截面的投影平衡方程。用基本體系方法計算時,是藉助於基本體系這個工具,以達到分步、分項寫出平衡方程的目的。
也可以不用基本體系,直接由轉角位移方程,寫出各桿件的桿端力表達式,在有結點角位移處,建立結點的力矩平衡方程;在有結點線位移處,建立截面的投影平衡方程。這些方程也就是位移法的基本方程。
3、求解步驟:
1)確定基本未知量;
2)由轉角位移方程,寫出各桿端力表達式;
3)在由結點角位移處,建立結點的力矩平衡方程,在由結點線位移處,建立截面的剪力平衡方程,得到位移法方程;
4)解方程,求基本未知量;
5)將已知的結點位移代入各桿端力表達式,得到桿端力;
6)按桿端力作彎矩圖。
4、排架計算(剪力分配法):
1)設Ji為排架柱的側移剛度係數。Ji是僅使柱頂發生單位側移時,在柱頂產生的剪力。一端固定一端鉸支 的桿的側移剛度是:Ji=3EI/h3;兩端固定桿的側移剛度是:Ji=12EI/h3。剪力分配係數;
2)當排架僅在柱頂受水平集中力P作用時,柱頂集中荷載P作為各柱的總剪力,按各柱的剪力分配係數μi進行比例分配,求出各柱剪力,再由反彎點開始即可作出彎矩圖。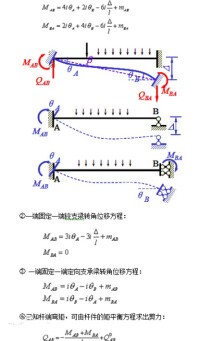

位移法
位移法的基本原理,是以在小變形的基礎的結構體系中,內力是可以疊加的,位移也是可以疊加的。結構中的受力、變形是可以分階段、分次發生的,分階段、分次發生的受力、變形是可以線性疊加的,疊加的結果與這些力、變形同時發生的結構所產生的內力、變形是相同的。
位移法的計算過程中,基本構件在單位荷載作用下的桿端內力、發生單位桿端變形時的桿端內力是十分重要的。所謂基本構件是指以特定形式支座為邊界條件的單跨梁,基本構件是各種梁、剛架的基本構成。根據力法的基本原理,可以計算出這些基本構件發生桿端單位位移或存在特定外部作用的情況下,桿端的內力指標。
這些指標通常稱為位移法常數。單位位移作用下產生的桿端力,可用力法求解,得到桿端內力,即形常數;僅由跨中荷載引起單跨超靜定梁的桿端內力稱為載常數,也叫固端力,載常數也可按力法計算出來。
超靜定結構分析(見桿繫結構的靜力分析)的基本方法之一,也稱變位法或剛度法,通常以結點位移作為基本未知數。位移法有兩種計算方式,一種是應用基本結構列出典型方程進行計算,另一種是直接應用轉角位移方程建立原結構上某結點或截面的靜力平衡方程進行計算,後者常稱為轉角位移法。
基本結構
用位移法計算超靜定結構時,須先確定基本未知數,即獨立的結點角位移和線位移的總數n(如圖1a,n=2。但忽略其軸向變形)。然後在這些結點上相應地加上阻止轉動的附加剛臂或阻止移動的附加鏈桿,使結構變成一系列離散部分的集合。這樣形成位移法的基本結構(如圖1b)。通常各離散部分均為等截面超靜定梁。位移法
典型方程
為使基本結構的變形和內力情況與原結構相同,必須使基本結構承受與原結構相同的荷載(包括溫度變化、支座沉陷等因素),並使附加約束髮生與原結構相同的位移。因為原結構上本無附加約束,所以基本結構上所有附加約束中的約束反力都應等於零。據此建立位移法典型方程:式中係數Knk表示在基本結構中第i個附加約束由於第k個附加約束髮生單位位移所引起的反力矩或反力,係數矩陣是對稱的;自由項RiP表示在結構上第i個附加約束由於荷載作用所引起的反力矩或反力;基本未知數xi是第i個結點的角位移或線位移,i=1,2,…,n。
為了求得典型方程中的係數和自由項,須分別繪製基本結構在各附加約束髮生單位位移時的Mi圖及在荷載作用下的MP圖,並利用結點或截面的平衡條件求出各係數和自由項。由於基本結構中各桿通常都是單跨超靜定梁,它們在荷載及支座發生各種單位位移情況下的固端彎矩公式都可以先行用力法或其他方法導出,這樣的公式稱為轉角位移方程。如等截面兩端固定梁當發生圖2所示的位移時,其轉角位移方程為式中i=EI/l;ψ=墹/l;E為材料彈性模量;I為截面慣性矩;MF為荷載引起的固端彎矩。對變截面桿也可以導出其轉角位移方程並繪製相應的圖表備用。位移法
轉角位移法
轉角位移法不必對基本結構分別作各Mi和MP圖,也不單獨計算各係數和自由項,而是直接應用轉角位移方程,將各桿端彎矩或剪力表示為未知結點位移的函數。然後依次截取各含有待求角位移的結點為隔離體,根據所有匯交於這一結點的各桿近端作用於該結點的彎矩及結點力矩荷載的代數和應等於零,而建立結點平衡方程;再依次作截面,截取各含有待求線位移結點的隔離體,在該線位移方向上列出力的投影的平衡方程,即得截面平衡方程,這樣建立起來的平衡方程與典型方程完全相同。
解算典型方程求得各基本未知數xi后,即可按疊加原理或轉角位移方程求得結構內力。
用位移法求解結構問題,第一步須列出物體內所有節點的全部廣義位移。這些廣義位移的總數目稱為節點位移自由度(又稱節點位移可動度)。例如圖中的平面剛架有3個節點:點1完全被約束,沒有廣義位移;點2有一個轉動位移;點3有一個轉動位移和一個水平方向的位移。因此該剛架的節點位移自由度為3。第二步是將結構的全部廣義位移加以約束,所得到的結構體系稱為基本體系。在基本體系的一個節點上解除某個廣義位移s的約束,此時如果在某個廣義位移r的方向上作用一個廣義力Krs,它在s方向上引起的廣義位移恰好為一個單位,則Krs稱為剛度係數。r為s時Krs稱為直接剛度係數;r不為s時稱為交叉剛度係數。它們可通過結構分析求出。求出各剛度係數后,把外載荷加到基本體繫上,就得到用節點未知廣義位移表示的位移法平衡方程組。方程數目恰與未知量數目相等,從而可以通過解方程組求出各節點的實際位移,進而可求得全部內力。
具有三個自由度的剛架
通常,用勢能原理來建立位移法平衡方程組,具體作法如下:
為系統的總勢能,式中xi(i=1,2,…,n)為節點未知廣義位移;Ri為載荷引起的第i個節點處的約束反力;dq為載荷作用點的位移;Kqq為在載荷作用點處產生單位廣義位移所需的廣義力;m為載荷個數;n為自由度。根據最小勢能原理,真實情況下的結構應滿足如下條件:
(i=1,2,…,n),
由此得到位移法平衡方程組:
或用矩陣表示為: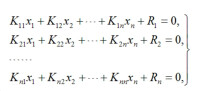
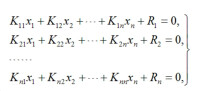
位移法
[K]{x}+{R}=0,
式中[K]為剛度矩陣;{x}對為廣義位移陣列;{R}為載荷陣列。上述方程組是關於n個未知量xi(i=1,2,…,n)的n個代數方程組,可解出xi(i=1,2,…,n)。
用位移法求解連續彈性體時,由於系統可看作是由無窮多個節點組成的,所以系統具有無窮多個節點位移自由度,這就需要無窮多個方程,因此必須用一些近似方程求解。方法之一是將系統化為有限個單元,只研究單元邊界處的位移,這就是有限元法。另一方法是假設位移為一級數形式,每項級數為一已知的滿足邊界條件的函數,其係數為未知常數,代入平衡微分方程后即可求得係數,從而得到位移。
在實際應用中,根據各類結構的特點,位移法已發展成為多種實用計演演算法,常用的有轉角位移法、變形分配法和力矩分配法等。
