共找到14條詞條名為結構力學的結果 展開
結構力學
基礎學科
結構力學(Structural Mechanics)是固體力學的一個分支,它主要研究工程結構受力和傳力的規律,以及如何進行結構優化的學科。結構力學研究的內容包括結構的組成規則,結構在各種效應(外力,溫度效應,施工誤差及支座變形等)作用下的響應,包括內力(軸力,剪力,彎矩,扭矩)的計算,位移(線位移,角位移)計算,以及結構在動力荷載作用下的動力響應(自振周期,振型)的計算等。結構力學通常有三種分析的方法:能量法,力法,位移法,由位移法衍生出的矩陣位移法後來發展出有限元法,成為利用計算機進行結構計算的理論基礎。
結構力學是一門古老的學科,又是一門迅速發展的學科。新型工程材料和新型工程結構的大量出現,向結構力學提供了新的研究內容並提出新的要求。計算機的發展,又為結構力學提供了有力的計算工具。另一方面,結構力學對數學及其他學科的發展也起了推動作用。有限元法這一數學方法的出現和發展就和結構力學的研究有密切關係。在固體力學領域中,材料力學給結構力學提供了必要的基本知識,彈性力學和塑性力學是結構力學的理論基礎。另外,結構力學與流體力學相結合形成邊緣學科——結構流體彈性力學。
評定結構的優劣,從力學角度看,主要是結構的強度和剛度。工程結構設計既要保證結構有足夠的強度,又要保證它有足夠的剛度。強度不夠,結構容易破壞;剛度不夠,結構容易皺損,或出現較大的振動,或產生較大的變形。皺損能夠導致結構的變形破壞,振動能夠縮短結構的使用壽命,皺損、振動、變形都會影響結構的使用性能,例如,降低機床的加工精度或減低控制系統的效率等。
很多工程結構是受到天然結構的啟發而創製出來的。人們在結構力學研究的基礎上,不斷創造出新的結構造型。加勁結構(見加勁板殼)、夾層結構(見夾層板殼)等都是強度和剛度比較高的結構。結構設計不僅要考慮結構的強度和剛度,還要做到用料省、重量輕。減輕重量對某些工程尤為重要,如減輕飛機的重量就可以使飛機航程遠、上升快、速度大、能耗低。

結構力學
到19世紀初,由於工業的發展,人們開始設計各種大規模的工程結構,對於這些結構的設計,要作較精確的分析和計算。因此,工程結構的分析理論和分析方法開始獨立出來,到19世紀中葉,結構力學開始成為一門獨立的學科。
19世紀30年代后,由於大量修建鐵路,相繼出現連續梁和各種桁架等結構形式,促進了連續梁和桁架的計算理論的發展。美國的S.惠普爾在1847年首先提出了桁架的計算理論,19世紀中出現了許多結構力學的計算理論和方法。法國的納維於1826年提出了求解靜不定結構問題的一般方法。這些理論形成了結構力學的初步基礎。從19世紀30年代起,由於要在橋樑上通過火車,不僅需要考慮橋樑承受靜載荷的問題,還必須考慮承受動載荷的問題,又由於橋樑跨度的增長,出現了金屬桁架結構。
從1847年開始的數十年間,學者們應用圖解法、解析法等來研究靜定桁架結構的受力分析,這奠定了桁架理論的基礎。1864年,英國的麥克斯韋創立單位載荷法和位移互等定理,並用單位載荷法求出桁架的位移,由此學者們終於得到了解靜不定問題的方法。基本理論建立后,在解決原有結構問題的同時,還不斷發展新型結構及其相應的理論。19世紀末到20世紀初,學者們對船舶結構進行了大量的力學研究,並研究了可動載荷下的粱的動力學理論以及自由振動和受迫振動方面的問題。
19世紀後半期,鋼結構已被廣泛應用,結構計算成了結構設計的必要步驟,計算理論也取得了很大進展。1864年J.C.麥克斯韋提出了超靜定結構的力法方程(見力法)。1879年A.卡斯蒂利亞諾在他的著作中論述了利用變形勢能求結構位移和計算超靜定結構的理論。1874~1885年間,O·莫爾發展了利用虛位移原理求位移的一般理論,至此分析結構位移及超靜定結構的一般理論日臻完善。

結構力學
到了20世紀20年代,人們又提出了蜂窩夾層結構的設想。根據結構的“極限狀態”這一概念,學者們得出了彈性地基上粱、板及剛架的設計計算新理論。對承受各種動載荷(特別是地震作用)的結構的力學問題,也在實驗和理論方面做了許多研究工作。隨著結構力學的發展,疲勞問題、斷裂問題和複合材料結構問題先後進入結構力學的研究領域。20世紀50年代出現了電子計算機后,結構力學的發展開始進入嶄新的階段。結構分析的矩陣法等數值方法因此獲得了迅速的發展,並編製了各種結構分析程序。隨後,在非線性分析、非彈性分析、結構抗震分析、結構抗環境作用分析等方面都取得了進展。更由於實驗技術的進步,結構模型試驗分析方法也取得了進展。 20世紀中葉,電子計算機和有限元法的問世使得大型結構的複雜計算成為可能,從而將結構力學的研究和應用水平提到了一個新的高度。

結構力學
觀察自然界中的天然結構,如植物的根、莖和葉,動物的骨骼,蛋類的外殼,可以發現它們的強度和剛度不僅與材料有關,而且和它們的造型有密切的關,很多工程結構就是受到天然結構的啟發而創製出來的。結構設計不僅要考慮結構的強度和剛度,還要做到用料省、重量輕.減輕重量對某些工程尤為重要,如減輕飛機的重量就可以使飛機航程遠、上升快、速度大、能耗低。
同樣材料力學、彈性力學、塑性力學等也研究桿件,但主要以各部分的應力為對象。由於計算技術的進步,處理問題的方法更加通用,現代結構力學研究的對象應該包括桿系、板、殼和連續體。過去,結構力學的任務偏重於結構分析,應以結構優化設計為主,研究如何選擇合理的截面,以達到結構的重量輕、造價低的目的。
在結構分析中,通常用簡化的圖形代替實際結構,稱為計算簡圖。結構可按計算簡圖的幾何特性及受力特性分成平面結構和空間結構,它們又可分為梁結構、桁架結構、拱結構(見拱)、剛架結構等,以及上述各種結構相互組合而成的組合體系。
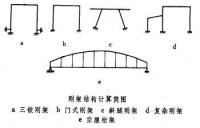
結構力學
①圖解法通過圖形表示作為矢量的力,並基於矢量的圖解原理求解靜定結構的反力和內力。
②解析法可分為力法、位移法和混合法。力法基於靜力平衡方程解靜定結構,並在補充變形協調方程后解超靜定結構。位移法以位移為基本未知數,基於轉角位移法及靜力平衡方程求解,然後再由位移求反力和內力。混合法是同時應用力法和位移法兩種概念求解的方法。
③能量法基於虛功原理、能量守恆定律、最小功原理等求解各種複雜問題(見能量原理)。此外,還應用各種數值分析方法(見有限元法)。
靜力學、動力學、流體力學、分析力學、運動學、固體力學、材料力學、複合材料力學、流變學、彈性力學、塑性力學、爆炸力學、磁流體力學、空氣動力學、理性力學、物理力學、天體力學、生物力學、計算力學、物理學、力學、熱學、光學、聲學、電磁學、核物理學、固體物理學。
一般對結構力學可根據其研究性質和對象的不同分為結構靜力學、結構動力學、結構穩定理論、結構斷裂、疲勞理論和桿繫結構理論、薄壁結構理論和整體結構理論等。
結構靜力學是結構力學中首先發展起來的分支,它主要研究工程結構在靜載荷作用下的彈塑性變形和應力狀態,以及結構優化問題。靜載荷是指不隨時間變化的外載入荷,變化較慢的載荷,也可近似地看作靜載荷。結構靜力學是結構力學其他分支學科的基礎。
結構動力學是研究工程結構在動載荷作用下的響應和性能的分支學科。動載荷是指隨時間而改變的載荷。在動載荷作用下,結構內部的應力、應變及位移也必然是時間的函數。由於涉及時間因素,結構動力學的研究內容一般比結構靜力學複雜的多。
結構穩定理論是研究工程結構穩定性的分支。現代工程中大量使用細長型和薄型結構,如細桿、薄板和薄殼。它們受壓時,會在內部應力小於屈服極限的情況下發生失穩(皺損或曲屈),即結構產生過大的變形,從而降低以至完全喪失承載能力。大變形還會影響結構設計的其他要求,例如影響飛行器的空氣動力學性能。結構穩定理論中最重要的內容是確定結構的失穩臨界載荷。
結構斷裂和疲勞理論是研究因工程結構內部不可避免地存在裂紋,裂紋會在外載荷作用下擴展而引起斷裂破壞,也會在幅值較小的交變載荷作用下擴展而引起疲勞破壞的學科。我們對斷裂和疲勞的研究歷史還不長,還不完善,但斷裂和疲勞理論發展很快。
在結構力學對於各種工程結構的理論和實驗研究中,針對研究對象還形成了一些研究領域,這方面主要有桿繫結構理論、薄壁結構理論和整體結構理論三大類。整體結構是用整體原材料,經機械銑切或經化學腐蝕加工而成的結構,它對某些邊界條件問題特別適用,常用作變厚度結構。隨著科學技術的不斷進展,又湧現出許多新型結構,比如20世紀中期出現的夾層結構和複合材料結構。
結構力學的研究方法主要有工程結構的使用分析、實驗研究、理論分析和計算三種。在結構設計和研究中,這三方面往往是交替進行並且是相輔相成的進行的。
使用分析就是在結構的使用過程中,對結構中出現的情況進行分析比較和總結,這是易行而又可靠的一種研究手段。使用分析對結構的評價和改進起著重要作用。新設計的結構也需要通過使用來檢驗性能。
實驗研究能為鑒定結構提供重要依據,這也是檢驗和發展結構力學理論和計算方法的主要手段。實驗研究分為三類:模型實驗、真實結構部件實驗、真實結構實驗。例如,飛機地面破壞實驗、飛行實驗和汽車的碰撞實驗等。
結構的力學實驗通常要耗費較多的人力、物力和財力,因此只能有限度地進行,特別是在結構設計的初期階段,一般多依靠對結構部件進行理論分析和計算。
在固體力學領域中,材料力學為結構力學的發展提供了必要的基本知識,彈性力學和塑性力學又是結構力學的理論基礎,另外結構力學還與其它物理學科結合形成許多邊緣學科,比如流體彈性力學等。
靜力學、動力學、流體力學、分析力學、運動學、固體力學、材料力學、複合材料力學、流變學、結構力學、彈性力學、塑性力學、爆炸力學、磁流體力學、空氣動力學、理論力學、物理力學、天體力學、生物力學、計算力學
主要物理學分支
物理學概覽、力學、熱學、光學、聲學、電磁學、核物理學、固體物理學
結構力學中的能量原理以內部和外部力量的能量或作業的形式表達應力,應變或變形,位移,材料特性和外部影響之間的關係。 由於能量是一個標量,這些關係為固體力學中可變形體的控制方程提供了方便和可選的方法。 它們也可以用於獲得相當複雜系統的近似解,繞過了解一組控制偏微分方程的困難任務。
