拓撲線性空間
拓撲線性空間
目錄
泛函分析早期所研究的空間大都是賦范線性的。但到了30年代初,人們已經充分地認識到,無論從巴拿赫空間理論本身,還是運算元代數的研究,都必須引進一般的,不只是序列收斂的弱拓撲。那時已經把巴拿赫空間的一些基本結果推廣到完備的、擬賦范的線性空間上去。其後,分佈理論的出現,又提出一批新空間如D空間、φ空間等等。這樣大量的重要空間就不再是賦范線性的了,於是有必要在它們的基礎上,建立起局部凸拓撲線性空間理論。從而開創了新的研究領域,也使泛函分析舊有的理論得到進一步發展。
設x 既是實或復的數域K上的線性空間,又是拓撲空間,並且x×x→x 的映射{x,y}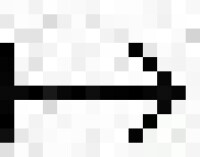 x+y和K×x→x 的映射{α,x}
x+y和K×x→x 的映射{α,x}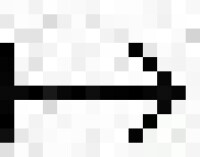 αx都是連續的,則稱x為拓撲線性空間。以下還假定所論拓撲線性空間是豪斯多夫空間,因為絕大多數有趣的定理和應用都是關於這類空間的。
αx都是連續的,則稱x為拓撲線性空間。以下還假定所論拓撲線性空間是豪斯多夫空間,因為絕大多數有趣的定理和應用都是關於這類空間的。
拓撲線性空間
拓撲線性空間
線性空間E中的點集A,如果當x,y∈A且0≤α≤1時αx+(1-α)y∈A,則稱A是凸集。設A與B是拓撲線性空間x中的點集,如果存在α>0使B嶅αA,則稱A吸收B。如果任何x∈x 都被M吸收,則稱M為吸收的點集。若對x∈M,當|λ|≤1時總有 λx∈M,則稱M是平衡的。顯然賦范線性空間中的點集 {x;‖x‖0使M嶅αV則稱M為有界集。
拓撲線性空間x為賦范的充要條件是 x的0點有凸的、有界的鄰域。
擬賦范空間 如果線性空間x上每個元x都恰有一數‖x‖與之對應,且①‖x‖≥0又‖x‖=0當且只當x=0;②‖-x‖=‖x‖, 又當 αn→α,‖xn-x‖→0 時有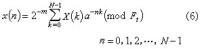 ;③‖x+y‖≤‖x‖+‖y‖,則稱x為擬賦范的線性空間。這是賦范線性空間的重要推廣。若x 還按距離d(x,y)=‖x-y‖是完備的,便稱x為F空間。【0,1】上全體幾乎處處是有限的,可測實值函數構成的集合S【0,1】按
;③‖x+y‖≤‖x‖+‖y‖,則稱x為擬賦范的線性空間。這是賦范線性空間的重要推廣。若x 還按距離d(x,y)=‖x-y‖是完備的,便稱x為F空間。【0,1】上全體幾乎處處是有限的,可測實值函數構成的集合S【0,1】按
拓撲線性空間
成為典型的F空間。F空間都是拓撲線性空間。
局部凸空間 如果拓撲線性空間x在0點存在由凸集構成的鄰域基,則稱x為局部凸拓撲線性空間,簡稱為局部凸空間。局部凸空間上必定存在非零的連續線性泛函。可以證明S【0,1】上沒有非零的連續線性泛函,從而S【0,1】便不是局部凸的。對於這樣的空間當然也就沒有對偶理論了。據此可見局部凸假設的重要性。
對局部凸空間x,可以證明存在x在原點之鄰域基,其中每個鄰域都是凸的、平衡的、吸收的。
若C是線性空間E中一個凸的,吸收的點集,則有所謂閔科夫斯基泛函
,
它具有性質:①ρ(x+y)≤ρ(x)+ρ(y),②當t≥0,ρ(tx)=tρ(x),③若又設C是平衡的,則ρ(αx)=|α|ρ(x)。一般也稱具有性質①與③的函數ρ(x)為半范數。
另一方面,於一族半范數,如果ρα(x)=0對一切α∈A都成立導致x=0,則全體{x|ραj(x)<ε,i=1,2,…,n},其中αi∈A,ε>0,便生成一個局部凸空間在0點的鄰域基。在應用上,許多局部凸空間正是這樣自然形成的。
完全的、可度量化的局部凸空間稱為弗雷歇空間。在文獻上,弗雷歇空間這個詞的使用是不統一的,也有不少人把前述F空間叫做弗雷歇空間。局部凸的空間x可度量化必須且只須 x上的拓撲能由可數多個半范數生成。巴拿赫空間上的運算元理論大部分可以推廣到弗雷歇空間上去。許多重要的空間是弗雷歇空間或者是由它們生成的,例如φ(Rn)空間、DK空間、D空間等等。
凸集 重要的哈恩-巴拿赫定理也可以表述為:若巴拿赫空間x 的線性簇 g(線性空間經平移后的集)與開球K不相交,則有閉超平面H使H叾g而H∩K=═(見巴拿赫空間)。上述g與K是很特殊的凸集。但對於有限維空間,H.閔科夫斯基在1911年便已論述了一般凸體的分離定理。對於局部凸拓撲線性空間x 有下述一般的分離定理:設A與B是x中非空的、不相交的凸集,則①若A含有內點,則有x上之非零連續線性泛函ƒ與實數r使Reƒ(x)≤r≤Reƒ(y)(當x∈A而y∈B);②若A是閉的,B是緊集,則有x上之連續線性泛函與實數r1,r2使得Reƒ(x)幾何學是拓撲線性空間論的特色。
端點 在凸性的研究中,很早就出現了端點這概念。後來發展成重要的端點方法。
設E是線性空間,═≠M吇K嶅E,如果從K中兩個點k1和k2的一個真凸組合,恆有k1,k2∈M,則稱M為K之端集。如果單點集{z0}是K的端集,則稱z0為K的端點。
設K是Rn中的緊凸集。閔科夫斯基證明每個x∈K都可表示成至多n+1個K之端點的凸組合。
起源於對巴拿赫空間的共軛空間中弱*緊集的研究,1940年證明了很有用的克列因-米利曼定理:設K是局部凸空間x中的緊集,又K之全體端點為ε,則K吇ε之凸閉包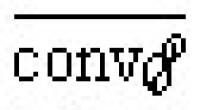 ,如果K還是凸的,則K=
,如果K還是凸的,則K=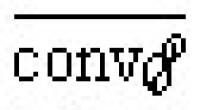 。
。
拓撲線性空間
拓撲線性空間
G.紹凱在1960年證明了如下定理:設K是度量空間x中凸的緊集,則K所有端點的集合ε是一個GΔ集合,且對每個x∈K,有定義在x之一切貝爾集上之非負的貝爾測度μx(·)使得μx(x\ε)=0,μx(ε)=1且。
弱拓撲與麥基拓撲 設x是線性空間,Y是x上一些線性泛函構成的線性空間,且Y能分離x的點,即ƒ(x)=0對一切 ƒ∈Y 都成立時導致x=0,便把這樣一對空間記作。
對於〈x,Y〉,則x上使Y中一切泛函都連續之最弱的局部凸拓撲便稱為x上的Y弱拓撲,記作σ(x,Y)。實際上,一切就構成 σ(x,Y)在0點的一個鄰域基。當x是巴拿赫空間時,則x上的弱拓撲即σ(X,X*),而x*上的弱拓撲即σ(x*,x)。
設線性空間x按拓撲J成為局部凸空間,記作(x,J)。所有在 x上按J連續的線性泛函稱為(x,J)的拓撲對偶,記作x*。在x上除了σ(x,Y)還可能有其他的局部凸拓撲J使(x,J)的拓撲對偶恰好是Y。人們自然希望能刻畫出所有這樣的拓撲J。
對於〈x,Y〉,則在Y之任何凸的,σ〈Y,x〉緊的點集上皆一致收斂的拓撲稱為x上的麥基拓撲,記作τ(x,Y),亦即必須且只須y(xα)在Y 之任何凸的σ(Y,x)緊的點集上都一致收斂。
拓撲τ(x,Y)比σ(x,Y)強。
麥基-阿倫斯定理 對於〈x,Y〉,則 x上之局部凸拓撲J使(x,J)的拓撲對偶恰好是Y的充要條件為σ(x,Y)吇J吇τ(x,y)。拓撲J也稱為〈x,Y〉拓撲。
對〈x,Y〉與M嶅x,則
稱為M的極集。當 x=Y 為希爾伯特空間,而M是x之子空間時,則 M0即 M寑。當x為巴拿赫空間,Y=x*而M={x|‖x‖≤r}時,則
。
布爾巴基-阿勞格魯定理 設U嶅x是O點之凸的、平衡的、某〈x,Y〉拓撲的鄰域,那麼U0是Y中σ(Y,x)緊集。
這是一般拓撲學在泛函分析中的重要成就。
對於一個重要的性質p,人們希望能完全地刻畫出使p得以成立的空間結構。這顯然是有趣的,事實上也往往是很有價值的。於是在拓撲線性空間論中便提出許多重要的空間,例如桶空間、蒙泰爾空間、核空間等等。
桶空間 局部凸空間x 中之平衡的,吸收的凸閉集叫做桶。如果x的每個桶都是O點的鄰域,則稱x 為桶空間。這空間的特性在於下列定理:設x 是局部凸空間,則x*中一切σ(x*,x)有界集皆同等連續的充要條件是x 為桶空間。凡屬第二綱的局部凸空間都是桶空間,於是巴拿赫空間,弗雷歇空間都是桶空間。廣義函數論中的D空間也是桶空間。
蒙泰爾空間 設x是桶空間。如果x中每個有界閉集都是緊的,則稱x為蒙泰爾空間。廣義函數論中之D空間與φ空間都是蒙泰爾空間。
有界型空間 如果局部凸空間x中任何凸的,平衡的,能吸收任何有界集的點集都是O點的鄰域,則稱x 為有界型空間。設線性運算元T 把有界型空間x 映入局部凸空間Y,如果T把每個有界集都映成有界集,則T是連續的。
正是由於研究映射的連續性,在局部凸拓撲線性空間論中便出現了種種拓撲和空間。前述之弱拓撲、麥基拓撲、有界型空間等都是如此。
核空間 設E為局部凸拓撲線性空間,V 是O點的一個凸的、平衡的鄰域。視{y|pV(x-y)=0}為一個元慜V,這裡 pV為對應於V的閔科夫斯基泛函。所有如此慜V按成為一個賦范線性空間xV。如果對O之任給的一凸的、平衡的鄰域U,都存在O 的凸的、平衡的鄰域V 使V嶅U且相應的典則映射的完備化空間 U為核運算元,則稱x為核空間,它是抽象核定理得以成立的局部凸空間,是數學分析中重要的拓撲線性空間。
U為核運算元,則稱x為核空間,它是抽象核定理得以成立的局部凸空間,是數學分析中重要的拓撲線性空間。
拓撲線性空間
由於數學及其應用的要求,人們往往要從熟知的空間,構造出新的拓撲線性空間。
歸納極限 設x是復(或實)線性空間,{xn} 都是局部凸空間,且 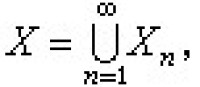 設xn上的局部凸拓撲是xn+1的拓撲在xn上的限制,設U是由x中所有那些凸的、平衡的、吸收的點集U組成,每個U∩xn 都是xn中的開集n=1,2,…,則U是一個局部凸拓撲在O點的鄰域基,這局部凸空間便稱為{xn}之嚴格歸納極限,這在廣義函數論中是很重要的概念。特點是:設T為從x到局部凸空間Y 的線性映射,則T是連續的必須且只須每個限制T|xn都連續。弗雷歇空間序列的嚴格歸納極限稱為LF空間,它是分析學中一類很有用的空間。
設xn上的局部凸拓撲是xn+1的拓撲在xn上的限制,設U是由x中所有那些凸的、平衡的、吸收的點集U組成,每個U∩xn 都是xn中的開集n=1,2,…,則U是一個局部凸拓撲在O點的鄰域基,這局部凸空間便稱為{xn}之嚴格歸納極限,這在廣義函數論中是很重要的概念。特點是:設T為從x到局部凸空間Y 的線性映射,則T是連續的必須且只須每個限制T|xn都連續。弗雷歇空間序列的嚴格歸納極限稱為LF空間,它是分析學中一類很有用的空間。
拓撲線性空間
投影拓撲 乘積拓撲(見拓撲空間)的推廣。設:{Eα}α∈A 是一族拓撲線性空間。設φα是一族從線性空間E到Eα的線性映射,則E上一切使φα(α∈A)都連續的拓撲中之最弱者稱為E上相對於{φα}α∈A的投影拓撲。
以桶空間這類型說,由它生成的商空間、乘積空間、嚴格歸納極限等都仍然是桶空間。一般對各種類型的空間,往往需要考察由它們生成的空間是否保持原來的類型不變。
參考書目
N.Bourbaki,Espaces Vectoriels Topologigues, Actualités Sei. Ind Hermann, Paris, 1953,1955.
J.L.Kelley and I.Namioka, et al.,Linear Topological Spaces, Van Nostrand,New York,1963.
G.Kthe,Topological Vector Spaces, Vo1. I,Springer-Verlag, New York, 1969.