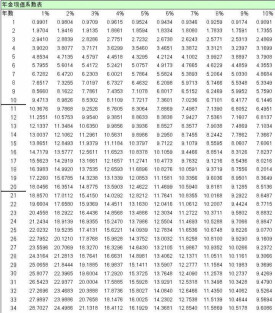
年金現值係數
金融領域的係數
年金現值係數,就是按利率每期收付一元錢折成的價值。
首先說什麼是年金,年金是每隔相等時間間隔收到或支付相同金額的款項,如每年年末收到養老金10000元,即為年金。年金現值是指按照一定的市場利率把發生期收到的各期年金利息折成現值之匯總。
年金現值係數公式:PVA/A =1/i-1/[i (1+i)^n]
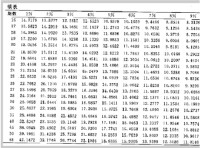
年金現值係數表
比如你在銀行裡面每年年末存入1200元,連續5年,年利率是10%的話,你這5年所存入資金的現值=1200*(1+10%)+1200*(1+10%)+1200*(1+10%)+1200*(1+10%)+1200*(1+10%)=7326.12
1200元就是年金,4548.96就是年金現值,1/10%-1/10%*1.1 =3.7908就是年金現值係數。
不同的報酬率、不同的期數下,年金現值係數是不相同的。
1、普通年金終值指一定時期內,每期期末等額收入或支出的本利和,也就是將每一期的金額,按複利換算到最後一期期末的終值,然後加總,就是該年金終值。例如:每年存款1元,年利率為10%,經過5年,逐年的終值和年金終值,可計算如下:
1元1年的終值=(1+10%)^1=1.100(元)
1元2年的終值=(1+10%)^2=1.210(元)
1元3年的終值=(1+10%)^3=1.331(元)
1元4年的終值=(1+10%)^4=1.464(元)
1元5年的終值=(1+10%)^5=1.611元
1元年金5年的終值=6.715(元)
如果年金的期數很多,用上述方法計算終值顯然相當繁瑣。由於每年支付額相等,折算終值的係數又是有規律的,所以,可找出簡便的計算方法。
設每年的支付金額為A,利率為i,期數為n,則按複利計算的年金終值S為:
S=A×(1+i)+…+A×(1+i)^n,(1)
等式兩邊同乘以(1+i):
S(1+i)=A(1+i)^2+…+A(1+l)^(n+1),(n等均為次方)(2)
上式兩邊相減可得:
S(1+i)-S=A(1+i)^(n+1)-A(1+i),
S=A[(1+i)^n-1]/i
式中[(1+i)n-1]/i的為普通年金、利率為i,經過n期的年金終值記作(S/A,i,n),可查普通年金終值係數表.
2、年金現值通常為每年投資收益的現值總和,它是一定時間內每期期末收付款項的複利現值之和。每年取得收益1元,年利率為10%,為期5年,上例逐年的現值和年金現值,可計算如下:
1年1元的現值=0.909(元)
2年1元的現值=0.826(元)
3年1元的現值=0.751(元)
4年1元的現值=0.683(元)
5年1元的現值=0.621(元)
1元年金5年的現值=3.790(元)
計算普通年金現值的一般公式為:
P=A/(1+i) +A/(1+i)…+A/(1+i) ,(1)
等式兩邊同乘(1+i)
P(1+i)=A+A/(1+i) +…+A/(1+i) ,(2)
(2)式減(1)式
P(1+i)-P=A-A/(1+i) ,
剩下的和上面一樣處理就可以了。
普通年金1元、利率為i,經過n期的年金現值,記作(P/A,i,n),可查年金現值係數表.
另外,預付年金、遞延年金的終值、現值以及永續年金現值的計算公式都可比照上述推導方法,得出其一般計算公式。