等式

含有等號的式子叫做等式(數學術語)。

形式：把相等的兩個數（或字母表示的數）用“=”連接起來。

等式可分為矛盾等式和條件等式。矛盾等式就是左右兩邊不相等的"等式"。也就是不成立的等式，比如5+2=8,實際上5+2=7,所以5+2=8是一個矛盾等式。有些式子無法判斷是不是矛盾等式，比如x-9=2，只有x=11時這個等式才成立(這樣的等式叫做條件等式)，x≠11時，這個等式就是矛盾等式。條件等式是指一些數量相等的關係。代數中所學的方程都是條件等式。

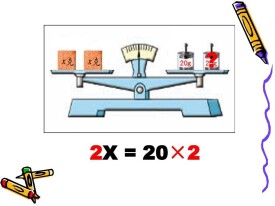
等式兩邊同時加上(或減去)同一個整式，等式仍然成立。

若a=b

那麼a+c=b+c

等式兩邊同時乘或除以同一個不為0的整式，等式仍然成立。

若a=b

那麼有a·c=b·c

或a÷c=b÷c （c≠0）

等式具有傳遞性。

若a1=a2,a2=a3,a3=a4,……an=an,那麼a1=a2=a3=a4=……=an

拓展1：等式兩邊同時被一個數或式子減，結果仍相等。

如果a=b，那麼c-a=c-b。

拓展2：等式兩邊取相反數，結果仍相等。

如果a=b，那麼-a=-b。

拓展3：等式兩邊不等於0時，被同一個數或式子除，結果仍相等。；

如果a=b≠0，那麼c/a=c/b。

拓展4：等式兩邊不等於0時，兩邊取倒數，結果仍相等。

如果a=b≠0，那麼1/a=1/b。

等式的性質是解方程的基礎，很多解方程的方法都要運用到等式的性質。如移項，運用了等式的性質1；去分母，運用了等式的性質2。

運用等式的性質，涉及除法時，要注意轉換后，除數不能為0，否則無意義。

恆等式（identities），數學概念，恆等式是無論其變數如何取值，等式永遠成立的算式。恆等式成立的範圍是左右函數定義域的公共部分，兩個獨立的函數卻各自有定義域，與x在非負實數集內是恆等的，而在實數集內是不恆等的。

它來源於e^ix=cosx+isinx(複數的三角表示),令x=π就得e^πi + 1 = 0。

“函數相等”與“恆等式”之間有什麼關係，由“恆等式”能得出“函數相等”嗎？

數學上，恆等式是無論其變數在給定的取值範圍內取何值，等式永遠成立的算式。恆等式有多個變數的，也有一個變數的，若恆等式兩邊就一個變數，恆等式就是兩個 解析式之間的一種關係。給定兩個解析式，如果對於它們的定義域（見函數）的公共部分（或公共部分的子集）的任一數或數組，都有相等的值，就稱這兩個解析式 是恆等的。

相關性質為：

1.若y=f(x)與y=g(x)有相同的定義域，對於定義域內的任一個x均有f(x)=g(x)則y=f(x)與y=g(x)是相等函數，同時兩解析式必相同。

2.若y=f(x)與y=g(x)是相等函數，則兩個函數的解析式相同，於是其中的參數都能對應相等。

一般地，用純粹的大於號“>”、小於號“<”連接的不等式稱為嚴格不等式，用不小於號（大於或等於號）“≥”、不大於號（小於或等於號）“≤”連接的不等式稱為非嚴格不等式，或稱廣義不等式。總的來說，用不等號(<,>,≥,≤,≠)連接的式子叫做不等式。

通常不等式中的數是實數，字母也代表實數，不等式的一般形式為F(x，y，……，z)≤G(x，y，……，z )（其中不等號也可以為<，≤,≥，> 中某一個），兩邊的解析式的公共定義域稱為不等式的定義域，不等式既可以表達一個命題，也可以表示一個問題。

1.下列式子可以用“=”連接的是( )

A.5+4_______12-5 B.7+(-4)______7-(+4) C.2+4×(-2)______-12 D.2×(3-4)_____2×3-4

2.下列等式變形錯誤的是( )

A.由a=b得a+5=b+5; B.由a=b得- a9 =- b9

C.由x+2=y+2得x=y; D.由-3x=-3y得x=-y

3.運用等式性質進行的變形，正確的是( )

A.如果a=b,那麼a+c=b-c; B.如果 ac = bc ,那麼a=b;

C.如果a=b,那麼ac = bc D.如果a2=3a,那麼a=3

答案：1:B，2:D，3:C