頻譜密度
頻譜密度
頻譜就是頻率的分佈曲線,複雜振蕩分解為振幅不同和頻率不同的諧振蕩,這些諧振盪的幅值按頻率排列的圖形叫做頻譜。設一個能量信號為s(t),則它的頻譜密度S(w)可以由傅里葉變換求得。
頻譜分析,是信號分析技術中的經典部分。尤其是自FFT信號分析儀得以應用以來,頻譜分析技術曾作為信號分析的主流技術而得到空前的發展,在工程領域被廣泛應用,解決了大量工程實際問題,即使現代信號分析技術大大發展,頻譜分析仍作為傳統和經典的信號分析技術而繼續被廣泛應用,並經常成為其他分析技術的參照。
任何錶現於時間或空間距離上有複雜振動的形式的變數,都可以分解為許多不同振幅和不同頻率的諧振,把這些諧振的振幅值按頻率(或周期)排列的圖形。可用作傳送信息的電磁波或振蕩的頻率集合。
頻譜就是頻率的分佈曲線,複雜振蕩可以分解為振幅不同和頻率不同的諧振蕩,這些諧振蕩的幅值按頻率排列的圖形叫做頻譜。廣泛應用在聲學、光學和無線電技術等方面。頻譜是頻率譜密度的簡稱。它將對信號的研究從時域引到頻域,從而帶來更直觀的認識。
設一個能量信號為 ,則它的頻譜密度可以由傅里葉變換求得: 。
能量信號的頻譜密度和功率信號的頻譜主要區別有:(1)頻譜密度是連續譜,而功率信號的頻譜是離散譜;(2)頻譜密度單位是幅度/頻率,而功率信號的頻譜單位是幅度;(3)能量信號的能量有限,並連續的分佈在頻率軸上,每個頻率點上的信號幅度是無窮小的,只有df上才有確定的非0振幅;(4)功率信號的功率有限,但能量無限,它在無限多的離散頻率點上有確定的非0振幅。
在進行頻譜的理論分析時,對周期信號 ,要用傅氏級數(FS)對其進行處理,得到: , 。其中,為周期信號 的頻譜函數。
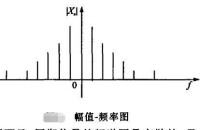
幅值-頻率圖
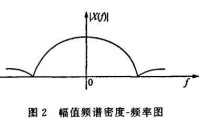
值頻譜密度-頻率圖
由圖可見,非周期信號的頻譜密度圖是連續的。其縱坐標表示信號的幅值密度,而不是諧波的幅值,其量綱是:信號量綱/Hz。
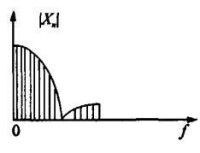
FFT譜圖
與周期函數的頻譜圖相似,信號的 的FFT譜是離散的,其幅值具有與信號相同的量綱。
由於是複函數,在工程應用中不夠方便,為此常將其與復共軛相乘,得到其功率譜(PowerSpectrum),即 ,其中: 是 的復共軛。功率譜是實函數,是 的平方,不僅使用方便而且其特徵更加突出。
當採用不同的頻率解析度進行信號分析時,儘管對其某一信號 的功率譜具有相似的波形,但其各點的功率譜值卻是不同的,越大,所得到的功率譜值也就越大。這樣不便於採用不同分析頻段(亦不同)時所得結果間的比較。於是,在信號分析儀上又定義了功率譜密度的概念,即: ,式中,為等效濾波器帶寬,是用頻率解析度乘以所選窗函數的窄帶修正因子。對於矩形窗、力窗和指數窗, 。
在某些工程中,還要用到能量譜的分析,於是在信號分析儀中又定義能量譜密度,即: ,其中:T為所分析信號的時間記錄長度。
(1)當對信號進行基於FT的理論分析時,對周期信號傅氏分解,得到其離散化的頻譜函數。而對非周期信號,應用傅氏變換,得到的是信號的頻譜密度函數。
(2)當使用FFT信號分析儀進行信號分析時。由於DFT的周期化處理,所得到的是信號的頻譜函數 ,而並非頻譜密度函數 。
(3)在信號分析儀上,功率譜密度是根據頻譜函數的運算而得到的,是為了方便工程運算結果的比
較,與理論分析中的頻譜密度函數不同。