傅氏級數

傅里葉級數的普通表達形式

假設{a0, a1, a2, a3, ..., an, ...}和{b1, b2, b3, ..., bn, ...}是一組無窮的常數。這些常數被稱為傅里葉係數。x是一個變數。普通的傅里葉級數可以表示為：

F(x) = a0/2 + a1 cos x + b1 sin x + a2 cos 2x + b2 sin 2x + ...+ an cos nx + bn sin nx + ...

理論波形與實際波形的比較

一些波形比較簡單，比如單純的正弦波，但是這些只是理論上的。在實際生活中，大多數波形都包含諧波頻率（最小頻率或基波頻率的倍數）的能量。諧波頻率能量相較於基波頻率能量的比例是依賴于波形的。傅里葉級數將這種波形數學的定義為相對於時間的位移函數（通常為振幅、頻率或相位）。

隨著傅里葉級數中計算的項的增加，級數會越來越近似於定義複雜信號波形的精確函數。計算機能夠計算出傅里葉級數的成百上千甚至數百萬個項。

傅里葉級數的收斂性：滿足狄利赫里條件的周期函數表示成的傅里葉級數都收斂。

狄利赫里條件如下：

在任何周期內，x(t)須絕對可積；

在任一有限區間中，x(t)只能取有限個極值點；

在任何有限區間上，x(t)只能有有限個第一類間斷點。

在x(t)的不可導點上，如果我們只取(1)式右邊的無窮級數中的有限項作和X(t)，那麼X(t)在這些點上會有起伏。一個簡單的例子是方波信號。

三 角函數族的正交性

所謂的兩個不同向量正交是指它們的內積為0，這也就意味著這兩個向量之間沒有任何相關性，例如，在三維歐氏空間中，互相垂直的向量之間是正交的。事實上，正交是垂直在數學上的的一種抽象化和一般化。一組n個互相正交的向量必然是線性無關的，所以必然可以張成一個n維空間，也就是說，空間中的任何一個向量可以用它們來線性表出。

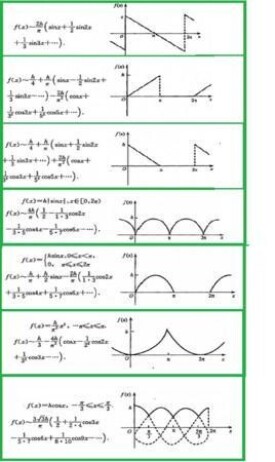
傅里葉級數的三角函數表達形式

設f(t)為一非正弦周期函數，其周期為T，頻率和角頻率分別為f , ω1。由於工程實際中的非正弦周期函數，一般都滿足狄里赫利條件，所以可將它展開成傅里葉級數。即

其中A0/2稱為直流分量或恆定分量；其餘所有的項是具有不同振幅，不同初相角而頻率成整數倍關係的一些正弦量。A1cos(ω1t+ψ1)項稱為一次諧波或基波，A1，ψ1分別為其振幅和初相角；A2cos(ω2t+ψ2)項的角頻率為基波角頻率ω1的2倍，稱為二次諧波，A2，ψ2分別為其振幅和初相角；其餘的項分別稱為三次諧波，四次諧波等。基波，三次諧波，五次諧波……統稱為奇次諧波；二次諧波，四次諧波……統稱為偶次諧波；除恆定分量和基波外，其餘各項統稱為高次諧波。式（10-2-1）說明一個非正弦周期函數可以表示一個直流分量與一系列不同頻率的正弦量的疊加。

上式有可改寫為如下形式，即

當A0，An, ψn求得后，代入式 (10-2-1)，即求得了非正弦周期函數f(t)的傅里葉級數展開式。

把非正弦周期函數f(t)展開成傅里葉級數也稱為諧波分析。工程實際中所遇到的非正弦周期函數大約有十餘種，它們的傅里葉級數展開式前人都已作出，可從各種數學書籍中直接查用。

從式（10-2-3）中看出，將n換成(-n)后即可證明有

a-徠n=an

b-n=-bn

A-n=An

ψ-n=-ψn

即an和An是離散變數n的偶函數，bn和ψn是n的奇函數。

將式（10-2-2）改寫為

可見 與 互為共軛複數。代入式（10-2-4）有

上式即為傅里葉級數的復指數形式。

下面對和上式的物理意義予以說明：

由式（10-2-5）得的模和輻角分別為

可見的模與幅角即分別為傅里葉級數第n次諧波的振幅An與初相角ψn，物理意義十分明確，故稱為第n次諧波的複數振幅。

的求法如下：將式（10-2-3a,b）代入式（10-2-5）有

上式即為從已知的f(t)求的公式。這樣我們即得到了一對相互的變換式（10-2-8）與（10-2-7），通常用下列符號表示，即

即根據式（10-2-8）由已知的f(t)求得，再將所求得的代入式（10-2-7），即將f(t)展開成了復指數形式的傅立葉級數。

在（10-2-7）中，由於離散變數n是從（-∞）取值，從而出現了負頻率（-nω1）。但實際工程中負頻率是無意義的，負頻率的出現只具有數學意義，負頻率（-nω1）一定是與正頻率nω1成對存在的，它們的和構成了一個頻率為nω1的正弦分量。

引入傅立葉級數復指數形式的好處有二：

（1）複數振幅同時描述了第n次諧波的振幅An和初相角ψn；

（2）為研究信號的頻譜提供了途徑和方便。

傅立葉係數包括係數，積分號和它的積分域，以及裡面的兩個周期函數的乘積——其中一個是關於f的，另一個是關於x的函數f(x),另一個則是和級數項n有關的三角函數值。這個三角函數可以是正弦，也可以是餘弦，因此傅立葉係數包括正弦係數和餘弦係數。其中當n=0時，餘弦值為1，此時存在一個特殊的係數，它只與x有關。正弦係數再成一個正弦，餘弦再乘一個餘弦，相加並且隨n求和，再加上一半的，就稱為了這個特別的函數f(x)的傅立葉級數。為什麼它特別呢，我想因為這裡只有它只限於一個周期函數而已，而級數的周期就是f(x)的周期，2 。

如果函數f(x)存在一個周期，但是不是2 了，而是關於y軸對稱的任意一個範圍，它還能寫成傅立葉級數么？也可以的。只要把傅立葉係數里的 換成l，並且把積分號里的三角函數中的n 下除一個l，同時把係數以外的那個n 底下也除一個l。其他的都不動。也可以認為，2 周期的傅立葉級數其實三角函數中x前面的係數應該是，其他的（積分域和係數）應該是x，只不過這時所有的l都是 罷了。

前面提及了，周期或是積分域，是關於y軸的一個任意範圍。其實周期函數不用強調這個，但是為什麼還要說呢？因為要特彆強調一下定義域是滿的。有些函數的定義域不是滿的，是0到l，當然這樣它有可能不是周期的。這些函數能寫成傅立葉級數么？同樣可以。而且，它的寫法不再是正弦和餘弦函數的累積，而是單獨的一個正弦函數或是餘弦函數。具體怎麼寫，就取決於怎麼做。因為域是一半的，所以自然而然想到把那一半補齊，f就成了周期函數。補齊既可以補成奇函數也可以補成偶函數。補成積函數，寫成的級數只有正弦項，即 為0。補成偶函數，寫成的級數就只含有餘弦項和第一項，即 為0。而，傅立葉係數相比非積非偶的函數要大一倍。

其實，如果不經延拓，上面那些對於奇偶函數同樣使用。

在做題時，常常看到級數後面跟著一個係數還有一個正弦函數，然後後面給出了這個係數很複雜的一串式子，這時候就容易突然短路了。但是如果再定睛一看，會發現其實那個係數不過是一個有積分的傅立葉係數而已。那麼一大串，應該看什麼呢？應當先看積分域，一下就可以定出周期了。第二步要明確級數和函數的關係即等價關係。函數不但包含在級數中，而且函數本身也是和級數等價的。但一般那個級數里的函數是一個擺設，不起什麼作用。

傅里葉變換能將滿足一定條件的某個函數表示成三角函數（正弦和/或餘弦函數）或者它們的積分的線性組合。在不同的研究領域，傅里葉變換具有多種不同的變體形式，如連續傅里葉變換和離散傅里葉變換。最初傅里葉分析是作為熱過程的解析分析的工具被提出的。

傅里葉變換屬於諧波分析。

傅里葉變換的逆變換容易求出，而且形式與正變換非常類似。

正弦基函數是微分運算的本徵函數，從而使得線性微分方程的求解可以轉化為常係數的代數方程的求解。在線性時不變的物理系統內，頻率是個不變的性質，從而系統對於複雜激勵的響應可以通過組合其對不同頻率正弦信號的響應來獲取。

卷積定理指出：傅里葉變換可以化複雜的卷積運算為簡單的乘積運算，從而提供了計算卷積的一種簡單手段。

離散形式的傅里葉變換可以利用數字計算機快速的實現（其演演算法稱為快速傅里葉變換演演算法（FFT））。