網路理論

圖論基礎上研究網路一般規律和網路流問題各種優化理論和方法的學科，是運籌學的一個分支。網路是用節點和邊聯結構成的圖，表示研究諸對象及其相互關係，如鐵路網、電力網和通信網等。網路中的節點代表任何一種流動的起點、運轉點和終點（如車站、港口、城鎮、計算機終端和工程項目的事件等）。網路中的邊代表任何物流、能流或信息流通過的通道（如輸電線、通信線、鐵路線和各事件之間的次序等）。在網路中每條邊上賦予某個正數，稱為該邊的權，它可以表示路程、流量、時間和費用等。建立網路的目的都在於把某種規定的物質、能量或信息從某個供應點最優地輸送到另一個需求點去。例如，在管道網路中要以最短的距離、最大的流量和最小的費用把水、石油或天然氣從供應點送到用戶那裡。

展概況 網路論源圖論。..基霍圖論矩陣論證網路律，即基霍流律壓律，僅圖論展貢獻，奠網路論基礎。紀，隨網路論廣泛，提優化計算。..福..富森提尋找流量標號算。..戴提尋找短徑標號算。，富森提求般費流狀態算，短徑、流量費流統，網路論基。繼提各類型網路流題，諸容量網路流、態流、增益流資流題，系列。

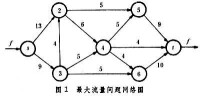
流量題 質流息流網路（圖）,流流量xij不超過該邊允許通過的流量cij的條件下，求出從發點s向收點t輸出的最大流量f，即在滿足和

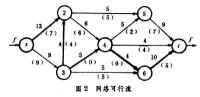
的條件下，使f最大。最大流量問題是一個特殊的線性規劃問題，有許多求解方法。一種有效的計算方法是福特-富爾克森法，它是根據最大流量-最小割集原理，通過標號演演算法，求出在上述約束條件下從發點s到收點t的最大流量f 的數值。其計算步驟如下：①繪製一個能滿足上述約束條件的網路可行流（圖2）。邊上的數字為允許流量cij，括弧內的數字為給定的可行流。②找出一條增廣鏈。增廣鏈是指從發點s到收點t的鏈中，滿足正向邊上和反向邊上的鏈。圖2中用粗線表示的{vs，v2,v3,v4,v6,vt} 是一條增廣鏈。其中【v2,v3】為反向邊，其餘均為正向邊。③調整可行流，即在增廣鏈的各邊上，屬正向邊加上一個修正量ε,屬反向邊減去一個修正量ε,即。εj值由下式決定：當時,；當時,。圖2中,，

。重複步驟②和③,當網路中不存在任何增廣鏈時，可行流即為最大流。圖3示出最大流，其最大流量。最大流問題可用於公路系統的車輛流、供水系統的水流、控制系統的信息流等。

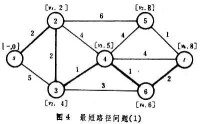
最短路徑問題 一般提法是：尋找網路中兩點間的最短路徑，即尋找連接這兩點的邊的總權數(可以是距離、時間、費用等)為最小的通路。圖4為最短路徑問題的一個例子。最短路徑問題有兩種演演算法。

①戴克斯特拉法　1959年提出。其計算方法是：從始點vs,標以零值，並記在vs旁的方括弧內。然後依節點序號順序找出到達各點的最短距離，並說明來自何方，例如在節點v3處標上【v2,4】,即表示來自節點v2，距離累計為4。戴克斯特拉法可以通過編製計算程序，在計算機上運算。

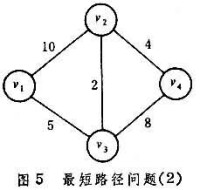
②海斯法　其計算公式如下：

式中d是從點vi到vj最多含有m 條邊的最短距離,vk是從點vi到vj所經過的中間點,n是網路中的節點數。對於圖5的例子，通過兩次運算可得最短矩陣【d】為

最短路徑問題可應用於貨物運輸、線路安裝、廠區布置、設備更新、場址選擇等優化問題。

網路理論

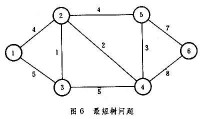
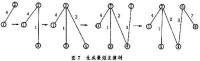
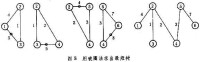
最短樹問題 圖6示出最短樹問題的一個例子。一城市擬在6個地點架設電纜線路，每條邊上的數字錶示兩點間的距離，要設計一個使電纜總長度為最短的鋪設方案。求解最短樹有兩種方法。①克羅斯卡爾法：從兩點間找出最短的邊聯結成一個最短支撐樹(圖7）。 ②破圈法：從網路的每一個圈中去掉具有最大權的邊，直到無圈時為止，即可求出最短樹（圖8）。上述例子的計算結果是：最短樹的總距離為17。最短樹問題的求解可用於城市煤氣和自來水管道、電話線、電纜等線路網路的優化問題。

最小費用流 在網路中，若每條邊【vi，vj】除容量cij外，還給一個數aij，表示從vi到vj運輸單位物資所需支付的費用，則問題便是尋找一個可行流{fij},其流值為給定的數值r*,並使總費用取最小值。這樣的可行流稱為最小費用流。最小費用流問題可用對應於線性規劃的原始演演算法和對偶演演算法求解。例如，若對偶演演算法是：從各邊流和流值的最小費用流開始，如果，則採用以費用作邊長求最短路徑的方法尋找關於{fij}的增廣鏈，把{fij}調整為流值r′(r＜r′≤r*)的最小費用流，直到流值為r*為止。

參考書目

陳樹柏：《網路圖論及其應用》，科學出版社，北京，1982。

L.R.Jr.Ford and D.R.Fulkerson,Flows in Networks，Princeton Univ. Press, N.J.,1962.

T.C.Hu,Integer Programming and Network Flows，Addison－Wesley Publ.Co.,1969.