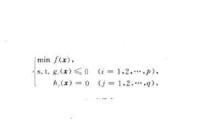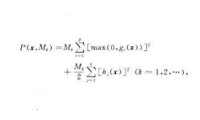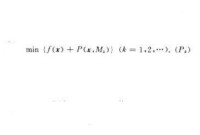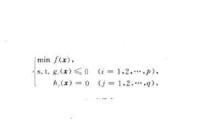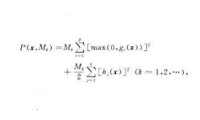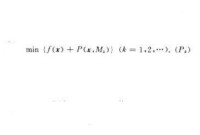外點法亦稱懲罰函數法或外懲罰函數法。將求解約束非線性規劃問題轉化為求解一系列無約束極小化問題的一類制約函數法。
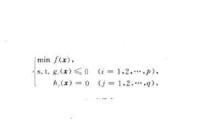
外點法
外點法(exterior point method)亦稱懲罰函數法或外懲罰函數法。將求解約束非線性規劃問題轉化為求解一系列無約束極小化問題的一類制約函數法(參見“制約函數法”).對於約束非線性規劃問 題(NP)
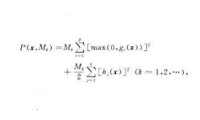
外點法
求解過程如下:選取一系列遞增的懲罰因子Mk(k= 1,2,wO,作相應懲罰函數列:
將求解問題(NP)轉化為求解一系列無約束極小化問題
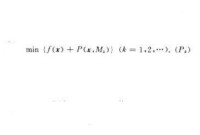
外點法
設xk是(Pk)的最優解,則在一定條件下可以證明點列{獷}存在極限點x",並且x’是問題(NP)的最優解。用此法求解(NP)是將“懲罰”加於不可行點,通過逐步增大懲罰因子Mk,迫使解的迭代點列{xk}從可行域外部向位於可行域邊界上的某最優解接近,所以稱為外點法。由於利用了
懲罰函數進行求解,故也稱懲罰函數法或外懲罰函數法.
外點法的經濟解釋是:一個採購者的經濟決策問題,即如果把
目標函數視為採購者決策時要花費的總“價格”數,
約束條件視為某種“規定”,採購者在“規定”範圍內買東西不罰款;若違反“規定”,則按罰款政策罰款。因此,採購者付出的總代價應是總的“價格”數與總的罰款數之和。採購者要以總代價作為最終目標。當把罰款政策定得非常苛刻時,即違反“規定”,則重罰,迫使採購者做決策時不敢違反“規定”,否則,他的總代價就不可能省。在數學上則表現在懲罰因子M*足夠大時,無約束極小化問題的最優解x’應該滿足諸約束條件,因而是約束極小化問 題的最優解.