割線

從圓外一點引圓的兩條割線，這一點到每條割線與圓交點的距離的積相等。

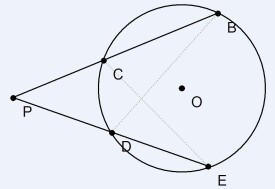
從圓外一點P引兩條割線與圓分別交於C,B,D,E,則有 PC·PB=PD·PE。如下圖所示。

(PA是切線）

割線定理為圓冪定理之一(切割線定理推論），其他二為：

切割線定理

如圖直線PB和PE是自點P引的⊙O的兩條割線，則PC·PB=PD·PE.

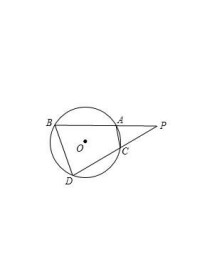
證明：連接CE、DB

∵∠E和∠B都對弧CD

∴由圓周角定理，得 ∠E=∠B

又∵∠EPC=∠BPD

∴△PCE∽△PDB

∴PC:PD=PE:PB, 也就是PC·PB=PD·PE.

割線定理與相交弦定理，切割線定理通稱為圓冪定理。

從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項。是圓冪定理的一種。

∵PT切⊙O於點T，PBA是⊙O的割線

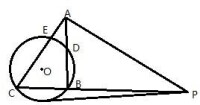
∴PT的平方=PA·PB（切割線定理）推論：

從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等

幾何語言：

∵PBA，PDC是⊙O的割線

∴PD·PC=PA·PB（切割線定理推論）(割線定理）

由上可知:PT的平方=PA·PB=PC·PD

切割線定理證明:

設ABP是⊙O的一條割線，PT是⊙O的一條切線，切點為T，則PT^2=PA·PB

證明：連接AT, BT

∵∠PTB=∠PAT(弦切角定理)

∠P=∠P(公共角)

∴△PBT∽△PTA(兩角對應相等，兩三角形相似)

則PB：PT=PT：AP

即：PT^2=PB·PA

相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們的推論統稱為圓冪定理。一般用於求直線段長度。

人們研究複數域上的解析函數時，常常需要研究函數在整個複平面的性質。然而，有些解析函數定義在複平面上時，表現出多值的性質，這樣的函數往往從一個點經過某些曲線回到這個點時，解析變化的函數值會跑到多值中另外的值上面。這樣的函數一方面可以採用黎曼曲面作為定義域，使得函數變為單值，另一方面，也可人為地在複平面上畫上一條線將複平面合適地割開，使得未被割開的區域內具有單值解析函數的良好性質。這樣的人為劃出的避免函數解析變化必然出現多值的線就叫割線.