懸魂梯
彭羅斯三角形的一個變式
彭羅斯階梯(Penrose Stairs),由萊昂內爾·彭羅斯( Lionel Penrose)和他的兒子羅傑·彭羅斯(Roger Penrose)創作。是彭羅斯三角形的一個變式。這是一個由二維圖形的形式表現出來的擁有4個90°拐角的四邊形樓梯。由於它是個從不上升或下降的連續封閉循環圖,所以一個人可以永遠在上面走下去而不會升高。顯然這在三維空間中是不可能的。
根據《龍嶺迷窟》記載:傳說中的懸魂梯,實際是一種非常厲害的機關術,但需要一些特定的條件,譬如:牆壁、台階、光線和幻影的配合等。
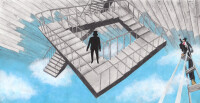
超級燈迷研究的懸魂梯模型
懸魂梯,以樓梯的四個角為A、B、C、D點,從其中任意一點下樓梯,最終都會回到原點,這就是《鬼吹燈》裡邊對“懸魂梯”的描述,胡八一遭遇的“懸魂梯”似乎應該是8字型的,不過那不重要,關鍵的問題是,這樣的情形到底有沒有可能在現實生活中發生?看法不一,其中有人提到,在黑暗的環境中,通過巧妙的使用陰影和特殊標誌將人引上岔路而毫無覺察,加上本來坡度很小,而石階很大,只要長度夠長,就會造成上坡和下坡的感覺不太分明,從而達到上面的效果。我比較贊同這種觀點,不過個人認為應該再加上一個條件,這個樓梯應該是有斜度的,只是斜度太小而不會被人察覺,這樣才有可能神不知鬼不覺的轉彎或是什麼。
《鬼吹燈》中懸魂梯的構造
懸魂梯的目的很明確,就是要把人困在裡面找不到出口。我覺得我們的主要的疑問有三個:
1、懸魂梯的形狀。
2、懸魂梯是怎樣讓人在裡面總是打轉,無法走出(主要是標記的問題)。
3、懸魂梯高低落差如何給人產生錯覺。那麼根據這幾個點,我們一起來抽絲剝繭,不一定非要下結論,我只是想通過這些疑問和推測找出比較符合邏輯的解決方式。
通過設立abcd四個頂點,a點大於b點大於c點大於d點得到a點一定大於d點即a點高度一定高於d點高度可得出懸魂梯不存在。
