共找到15條詞條名為ICA的結果 展開
ICA
獨立成分分析
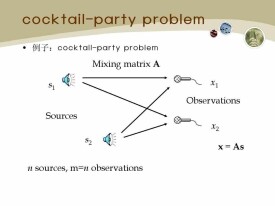
ICA(Independent Component Correlation Algorithm)是一種函數，X為n維觀測信號矢量，S為獨立的m（m<=n)維未知源信號矢量，矩陣A被稱為混合矩陣。ICA的目的就是尋找解混矩陣W（A的逆矩陣），然後對X進行線性變換，得到輸出向量U。
最簡單的即為最近鄰分類器（NNC）：用距離參數表示訓練集模板與測試樣本的差異，認為測試樣本與滿足最小距離的訓練樣本屬於同一種表情。
目錄
獨析簡介
=
==
(1)對輸入數據進行中心化和白化預處理
X*=X-u
經過白化變換后的樣本數據為
Z=Wz X*
(2)從白化樣本中求解出解混矩陣W
通過優化目標函數的方法得到W
(3)得到獨立的基向量U
U=WX
應用：表情分類
得到基向量U后，任何一個樣本可用U的線性組合來表示。
線性組合的係數即Xi向U上的投影係數：
Ei=UXi'
訓練樣本和測試樣本可分別得到Ei和Etest。
然後選擇合適的分類器，就可以進行分類。
function [Out1, Out2, Out3] = fastica(mixedsig, varargin)
%FASTICA(mixedsig) estimates the independent components from given
% multidimensional signals. Each row of matrix mixedsig is one
% observed signal.
% = FASTICA (mixedsig); the rows of icasig contain the
% estimated independent components.
% = FASTICA (mixedsig); outputs the estimated separating
% matrix W and the corresponding mixing matrix A.
mixedsig為輸入向量，icasig為求解的基向量。
A即為混合矩陣，可以驗證mixedsig=A×icasig。
W即為解混矩陣，可以驗證icasig=W×mixedsig。
基本信息
- 外文名
- independent component analysis
- 應用
- 表情分類
- 等式
- U=WX=WAS
- 中文
- 獨立成分分析