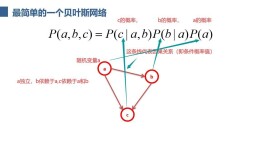
貝葉斯法則

貝葉斯法則概述圖。

貝葉斯法則又被稱為貝葉斯定理、貝葉斯規則是概率統計中的應用所觀察到的現象對有關概率分佈的主觀判斷（即先驗概率）進行修正的標準方法。

所謂貝葉斯法則，是指當分析樣本大到接近總體數時，樣本中事件發生的概率將接近於總體中事件發生的概率。

但行為經濟學家發現，人們在決策過程中往往並不遵循貝葉斯規律，而是給予發生的事件和最新的經驗以更多的權值，在決策和做出判斷時過分看重的事件。面對複雜而籠統的問題，人們往往走捷徑，依據可能性而非根據概率來決策。這種對經典模型的系統性偏離稱為“偏差”。由於心理偏差的存在，投資者在決策判斷時並非絕對理性，會行為偏差，進而影響資本市場上價格的變動。但長期以來，由於缺乏有力的替代工具，經濟學家不得不在分析中堅持貝葉斯法則。

通常，事件A在事件B(發生)的條件下的概率，與事件B在事件A的條件下的概率是不一樣的；然而，這兩者是有確定的關係，貝葉斯法則就是這種關係的陳述。

作為一個規範的原理，貝葉斯法則對於所有概率的解釋是有效的；然而，頻率主義者和貝葉斯主義者對於在應用中概率如何被賦值有著不同的看法：頻率主義者根據隨機事件發生的頻率，或者總體樣本裡面的個數來賦值概率；貝葉斯主義者要根據未知的命題來賦值概率。一個結果就是，貝葉斯主義者有更多的機會使用貝葉斯法則。

貝葉斯法則是關於隨機事件A和B的條件概率和邊緣概率的。

\Pr(A|B)=\frac{\Pr(B|A)\,\Pr(A)}{\Pr(B)}\propto L(A|B)\,\Pr(A)\!

其中L(A|B)是在B發生的情況下A發生的可能性。

在貝葉斯法則中，每個名詞都有約定俗成的名稱：

Pr(A)是A的先驗概率或邊緣概率。之所以稱為"先驗"是因為它不考慮任何B方面的因素。

Pr(A|B)是已知B發生后A的條件概率，也由於得自B的取值而被稱作A的后驗概率。

Pr(B|A)是已知A發生后B的條件概率，也由於得自A的取值而被稱作B的后驗概率。

Pr(B)是B的先驗概率或邊緣概率，也作標準化常量（normalized constant）。

按這些術語，Bayes法則可表述為：

后驗概率=(相似度*先驗概率)/標準化常量

也就是說，后驗概率與先驗概率和相似度的乘積成正比。

另外，比例Pr(B|A)/Pr(B)也有時被稱作標準相似度（standardised likelihood），Bayes法則可表述為：后驗概率=標準相似度*先驗概率

全壟斷市場，只有一家企業A提供產品和服務。企業B考慮是否進入。當然，A企業不會坐視B進入而無動於衷。B企業也清楚地知道，是否能夠進入，完全取決於A企業為阻止其進入而所花費的成本大小。

挑徠戰者B不知道原壟斷者A是屬於高阻撓成本類型還是低阻撓成本類型，但B知道，如果A屬於高阻撓成本類型，B進入市場時A進行阻撓的概率是20%（此時A為了保持壟斷帶來的高利潤，不計成本地拚命阻撓）；如果A屬於低阻撓成本類型，B進入市場時A進行阻撓的概率是100%。

博弈開始時，B認為A屬於高阻撓成本企業的概率為70%，因此，B估計自己在進入市場時，受到A阻撓的概率為：

0.7×0.2+0.3×1=0.44

0.44是在B給定A所屬類型的先驗概率下，A可能採取阻撓行為的概率。

當B進入市場時，A確實進行阻撓。使用貝葉斯法則，根據阻撓這一可以觀察到的行為，B認為A屬於高阻撓成本企業的概率變成A屬於高成本企業的概率=0.7（A屬於高成本企業的先驗概率）×0.2（高成本企業對新進入市場的企業進行阻撓的概率）÷0.44=0.32

根據這一新的概率，B估計自己在進入市場時，受到A阻撓的概率為：

0.32×0.2+0.68×1=0.744

如果B再一次進入市場時，A又進行了阻撓。使用貝葉斯法則，根據再次阻撓這一可觀察到的行為，B認為A屬於高阻撓成本企業的概率變成

A屬於高成本企業的概率=0.32（A屬於高成本企業的先驗概率）×0.2（高成本企業對新進入市場的企業進行阻撓的概率）÷0.744=0.086

這樣，根據A一次又一次的阻撓行為，B對A所屬類型的判斷逐步發生變化，越來越傾向於將A判斷為低阻撓成本企業了。

以上例子表明，在不完全信息動態博弈中，參與人所採取的行為具有傳遞信息的作用。儘管A企業有可能是高成本企業，但A企業連續進行的市場進入阻撓，給B企業以A企業是低阻撓成本企業的印象，從而使得B企業停止了進入地市場的行動。

應該指出的是，傳遞信息的行為是需要成本的。假如這種行為沒有成本，誰都可以效仿，那麼，這種行為就達不到傳遞信息的目的。只有在行為需要相當大的成本，因而別人不敢輕易效仿時，這種行為才能起到傳遞信息的作用。

傳遞信息所支付的成本是由信息的不完全性造成的。但不能因此就說不完全信息就一定是壞事。研究表明，在重複次數有限的囚徒困境博弈中，不完全信息可以導致博弈雙方的合作。理由是：當信息不完全時，參與人為了獲得合作帶來的長期利益，不願過早暴露自己的本性。這就是說，在一種長期的關係中，一個人干好事還是幹壞事，常常不取決於他的本性是好是壞，而在很大程度上取決於其他人在多大程度上認為他是好人。如果其他人不知道自己的真實面目，一個壞人也會為了掩蓋自己而在相當長的時期內做好事。

考慮一個醫療診斷問題，有兩種可能的假設：（1）病人有癌症。（2）病人無癌症。樣本數據來自某化驗測試，它也有兩種可能的結果：陽性和陰性。假設我們已經有先驗知識：在所有人口中只有0.008的人患病。此外，化驗測試對有病的患者有98%的可能返回陽性結果，對無病患者有97%的可能返回陰性結果。

上面的數據可以用以下概率式子表示：

P(cancer)=0.008,P(無cancer)=0.992

P(陽性|cancer)=0.98,P(陰性|cancer)=0.02

P(陽性|無cancer)=0.03，P(陰性|無cancer)=0.97

假設有一個新病人，我們判斷他檢驗出陽性的可能性大還是陰性的可能性大呢？我們可以來計算極大后驗假設：

P(陽性)=P(陽性|cancer)p(cancer)+P(陽性|無cancer)P(無cancer)=0.98*0.008+0.03*0.992=0.0078+0.02976=0.03756

P(陰性)=P(陰性|無cancer)*p(無cancer)+P(陰性|cancer)P(cancer)=0.97*0.992+0.008*0.02=0.96224+0.00016=0.96244

因此，陰性的可能性大。

海薩尼轉換與貝葉斯法則

1967年，海薩尼（JohnHarsanyi)指出所有老定義下具有不完全信息的博弈都可以在不改變其精髓的情況下被重新模型化為一個完全但不完美的信息博弈，這一切只需要添加一個由自然在不同規則集合中進行選擇的初始行動即可。在老的定義中，博弈論學家常指出不完全信息博弈是不可分析的，而海薩尼的創見使得這一切有所改變。老的定義是這樣描述的：在完全信息博弈中，全體參與人都知道博弈的規則，否則這一博弈就是一個不完全信息博弈。儘管海薩尼未指出老的定義是有問題的，但事實上人們的觀點已經發生了變化，認為在原有定義中，被轉換后的博弈才是不完全信息博弈。在博弈中，其中有參與人也許對博弈的支付並不十分清楚，但對支付還是有一定的了解的。一般情況下，採用主觀概分佈來表示信息。也就是基於概率對進行分組構建各種博弈支付，可以形成一個特定的支付集合。比如甲與乙選擇策略時，可以這樣考慮，甲選擇某一種策略時，乙選擇策略有幾種，乙的這些策略按發生的概率進行分組。通常構建一個博弈樹就可以較好地表達這一切。海薩尼教義的觀點關鍵在於假定所有的參與人都是有共同的認識，對於策略採取發生的概率是一個共同知識。隱含的意思也就是：參與人對於自己的猜測至少是少許公開了的。

在對一個博弈的信息結構進行劃分的時候，並不試圖決定參與人能從其它參與人的行動中推斷出些什麼東西。先驗概率是作為博弈規則的一部分存在，因此，一個參與人必須是持有關於其它參與人類型的先驗信念，同時，在觀察到他們的行動后，就要假定他們遵循著均衡的行為，然後更新自己的信念。

用P(h)表示在沒有訓練數據前假設h擁有的初始概率。P(h)被稱為h的先驗概率。先驗概率反映了關於h是一正確假設的機會的背景知識如果沒有這一先驗知識，可以簡單地將每一候選假設賦予相同的先驗概率。類似地，P(D)表示訓練數據D的先驗概率，P(D|h)表示假設h成立時D的概率。機器學習中，我們關心的是P(h|D)，即給定D時h的成立的概率，稱為h的后驗概率。

學習器在候選假設集合H中尋找給定數據D時可能性最大的假設h，h被稱為極大后驗假設（MAP）確定MAP的方法是用貝葉斯公式計算每個候選假設的后驗概率，計算式如下:

h_map=argmaxP(h|D)=argmax(P(D|h)*P(h))/P(D)=argmax P(D|h)*p(h)(h屬於集合H)

最後一步，去掉了P(D)，因為它是不依賴於h的常量。

在某些情況下，可假定H中每個假設有相同的先驗概率，這樣式子可以進一步簡化，只需考慮P(D|h)來尋找極大可能假設。

h_ml=argmaxp(D|h)h屬於集合H

P(D|h)常被稱為給定h時數據D的似然度，而使P(D|h)最大的假設被稱為極大似然假設。

(1)貝葉斯分類並不把一個對象絕對地指派給某一類，而是通過計算得出屬於某一類的概率，具有最大概率的類便是該對象所屬的類；

(2)一般情況下在貝葉斯分類中所有的屬性都潛在地起作用，即並不是一個或幾個屬性決定分類，而是所有的屬性都參與分類；

(3)貝葉斯分類對象的屬性可以是離散的、連續的，也可以是混合的。

貝葉斯定理給出了最小化誤差的最優解決方法，可用於分類和預測。理論上，它看起來很完美，但在實際中，它並不能直接利用，它需要知道證據的確切分佈概率，而實際上我們並不能確切的給出證據的分佈概率。因此我們在很多分類方法中都會作出某種假設以逼近貝葉斯定理的要求。